30-minute Global Maths & Science Lesson 2021 Fraction Wall Games
BUILD A FRACTION WALL
This wall is 1 unit wide. It shows one unit and two half units.
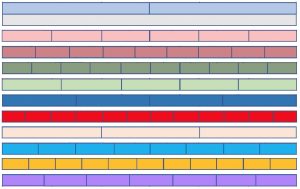 Click here to download the FRACTION WALL 30-minute lesson instructions and worksheet. Cut out the strips. Rearrange the order of the strips to build a wall with smaller and smaller blocks in each layer as it is built up. Label the blocks 1,\frac{1}{2},\frac{1}{3}, \frac{1}{4},\frac{1}{5}, \frac{1}{6},\frac{1}{7}, \frac{1}{8},\frac{1}{9}, \frac{1}{10}, \frac{1}{11} and \frac{1}{12}.
Click here to download the FRACTION WALL 30-minute lesson instructions and worksheet. Cut out the strips. Rearrange the order of the strips to build a wall with smaller and smaller blocks in each layer as it is built up. Label the blocks 1,\frac{1}{2},\frac{1}{3}, \frac{1}{4},\frac{1}{5}, \frac{1}{6},\frac{1}{7}, \frac{1}{8},\frac{1}{9}, \frac{1}{10}, \frac{1}{11} and \frac{1}{12}.
Explain how the wall shows that one half, two quarters and three sixths are equivalent fractions \frac{1}{2}=\frac{2}{4}=\frac{3}{6}.
Explain how the wall shows that three quarters is greater than two thirds \frac{3}{4}>\frac{2}{3}.
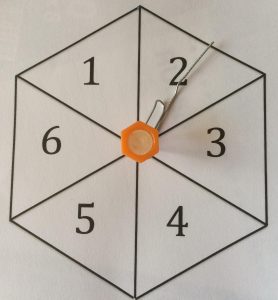
PLAY THE FRACTION WALL DOUBLE SIX GAME
To play this starter game you need 2 dice or a spinner and this fraction wall showing fractions 1,\frac{1}{2},\frac{1}{3}, \frac{1}{4},\frac{1}{5} and \frac{1}{6}.
Play with 2 players or 2 teams. If you are a small group of 7 or fewer people, then everyone can play individually and, in turn, throw the dice for themselves.
Players throw 2 dice or use a spinner, and make a fraction with the numbers on the dice putting the smaller number on top. For example, a 2 and a 3 make \frac{2}{3}.
Use the Fraction Wall to compare the fractions. The largest fraction wins the round and scores a point. More than one player may score a point in the same round if they get the largest fraction.
 VARIATIONS OF THE FRACTION WALL
VARIATIONS OF THE FRACTION WALL
If time, play with walls of different heights that include smaller fractions. You will need to make spinners that show the digits needed for your game. The instructions show how to make your own spinner with digits 1 to 9 for the Fraction Wall Game on a wall built up to the layer of ninths on top.
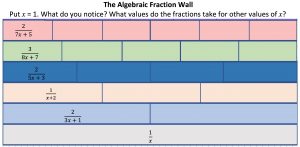
The rules for the Algebraic Fraction Wall Game are similar. Each player throws 2 dice or spins a 1 to 6 spinner twice. The value of x is given by one die or the first spin. The level is given by the other die or the second spin. For example if Player A throws a 5 followed by 2 (x = 5 and LEVEL 2) and Player B throws 4 followed by 5 (x = 4 and LEVEL 5) then Player A has the larger fraction and wins that round because \frac{2}{16}=\frac{1}{8}>\frac{3}{39}=\frac{1}{13}.
Click here to download a sheet of fraction walls.
Click here to download a copy of the Algebraic Fraction Wall
Click here to download the FRACTION WALL Inclusion and Home Learning Guide
Click here to download the Notes for Teachers.
Follow up Primary and Lower Secondary
Chocolate fractions https://aiminghigh.aimssec.ac.za/chocolate-fractions/
Fractions by Halves https://aiminghigh.aimssec.ac.za/fractions-by-halves/
Fractions by Thirds https://aiminghigh.aimssec.ac.za/fractions-by-thirds/
Tangram Fractions https://aiminghigh.aimssec.ac.za/tangram-fractions/
Fraction Jigsaw https://aiminghigh.aimssec.ac.za/fraction-jigsaw/
Divide Divide https://aiminghigh.aimssec.ac.za/divide-divide/
Repetition https://aiminghigh.aimssec.ac.za/repetition/
Egyptian Fractions https://aiminghigh.aimssec.ac.za/egyptian-fractions/
The Greedy Algorithm https://aiminghigh.aimssec.ac.za/the-greedy-algorithm/
Upper Secondary
Peaches https://aiminghigh.aimssec.ac.za/peaches/
GP Algebraically https://aiminghigh.aimssec.ac.za/gp-algebraically/
GP Geometrically https://aiminghigh.aimssec.ac.za/gp-geometrically/
Continued Fractions 1 https://nrich.maths.org/1351
Continued fractions 2 https://nrich.maths.org/1352
Farey Sequences https://aiminghigh.aimssec.ac.za/farey-sequences/
Mediant Madness https://nrich.maths.org/831
Ford Circles https://nrich.maths.org/6594
Farey Neighbours https://nrich.maths.org/6598
Approximations, Euclid’s Algorithm and Continued fractions https://nrich.maths.org/1397
South Africa COVID-19 News
Here is the official website for COVID-19 updates.
Login
SUPPORT AIMSSEC