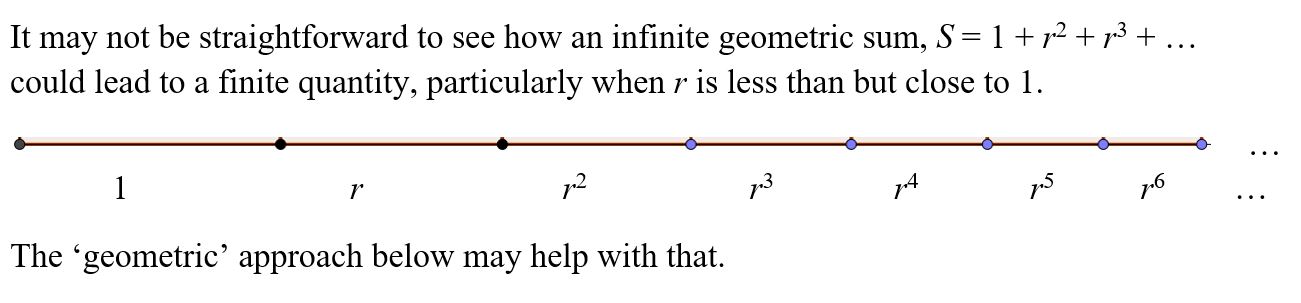The squares in the diagram are to help us visualise an infinite geometric sum and we are not summing the areas of the squares, simply the lengths along the x-axis. The squares have side lengths given by powers of r: 1, r, r^2, … where 0 < r < 1 .
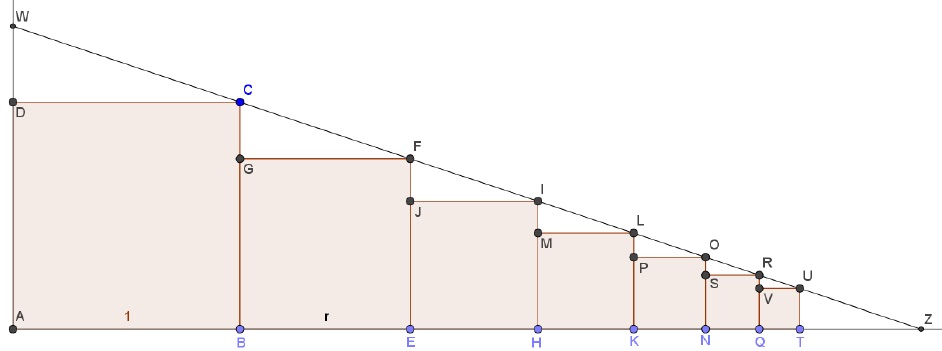1. Show that the right angled triangles on top of each square are all similar. You can start with ΔCGF and ΔFJI and express the horizontal and vertical sides in terms of 1 and r. Similar arguments should work for all subsequent triangles.
2. How does this establish that the top-right vertices of the squares (C, F, I, L, …) all lie on the same straight line?
3. Extend the line CF to intersect the x-axis at Z and the y-axis at W.
4. Calculate the length DW using the fact that ΔCGF and ΔWDC are similar. Hence find the length AW.
5. What can you say about ΔWAZ?
6. What can you say about length AZ? Use your above work to find the length AZ and hence establish that 1+ r + r^2 + … is finite and equals \frac{1}{1-r}.
If you enjoyed this article, please consider sharing it!
FOLLOW US ON SOCIAL MEDIA
