Egyptian Fractions

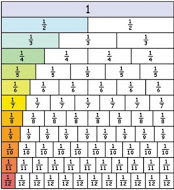Egyptian fractions are unit fractions, that is fractions with a numerator of 1. We are going to investigate methods of reducing all fractions to the sums of different smaller unit fractions as we see in this example:\frac{5}{12}= \frac{1}{3}+\frac{1}{12}\\ \frac{3}{4}=\frac{1}{2}+\frac{1}{4}...

Try some for yourself. Check your answers using a Fraction Wall. Does this always work? Could you explain to someone else how to use this method?

For a fraction \frac{a}{b} find the largest unit fraction smaller than \frac{a}{b} and subtract it. Repeat this process until you get a unit fraction. For example \frac{1}{3}<\frac{3}{7}<\frac{1}{2} and \frac{3}{7}-\frac{1}{3}=\frac{2}{21}

\frac{1}{11}<\frac{2}{21}<\frac{1}{10} and \frac{2}{21}-\frac{1}{11}=\frac{1}{231}  so

However, there are different ways to reduce unit fractions to the sums of different smaller unit fractions. For example \frac{1}{6}= \frac{1}{7}+\frac{1}{42}\\   \frac{1}{6}=\frac{1}{8}+\frac{1}{24}\\ \frac{1}{6}=\frac{1}{9}+\frac{1}{18}\\ \frac{1}{6}=\frac{1}{10}+\frac{1}{15}\\ \frac{1}{6}=\frac{1}{11}+\frac{1}{14}+\frac{1}{231}....

Can all unit fractions be made up in more than one way like this? Why? Try some examples of your own to test out your ideas.

Click here for Notes for Teachers.