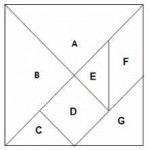This is a classic Chinese Tangram. Each of the people illustrated, and thirteen convex polygons, can be made with the 7 pieces and there are hundreds of other puzzles based on this tangram.
Can you find a way to fold a sheet of paper so that you can cut out the tangram pieces accurately without any measuring?
Take the edge length of the square as 1 unit.
- Find the areas of the 7 pieces. What fraction of the square does each piece make? What are the perimeters of the 7 pieces?
- Arrange the 7 pieces in order of their areas.
- Arrange the 7 pieces in order of their perimeters.
- Are these two orders the same?
- Make a square from the pieces A, G, C and E. What is its area? What is its edge length?
- How many different polygons can you make using all 7 pieces of the tangram.
TANGRAM FRACTION GAME
You will need 7 tangram pieces. Draw a square frame into which the pieces fit.
Make 8 identical fraction cards. Write \frac {1}{4}, \frac {1}{4}, \frac {1}{8}, \frac {1}{8}, \frac {1}{8}, \frac {1}{16}, \frac {1}{16} on 7 cards
and leave one card blank. Put the cards in a bag or in a box and shake to mix the cards, or place the cards face down on the table and mix them.
Take the tangram pieces out of the frame. Each player (or team) in turn picks a fraction card, selects a tangram piece with area corresponding to the fraction on the card, notes the area, and places the piece in position in the frame. The winner is the player with the greatest total area when the 7 pieces are back in the frame and all 8 cards have been taken.
Click here for the TANGRAM FRACTIONS poster.
Click here for the Inclusion and Home Learning Guide.
Click here for the TANGRAM FRACTIONS worksheet.
Click here for the AIMSSEC TANGRAM FRACTIONS Notes for Teachers
For a bit of fun see http://nrich.maths.org/1491
If you enjoyed this article, please consider sharing it!
4 Responses to Tangram Fractions and Game
Leave a Reply
You must be logged in to post a comment.
FOLLOW US ON SOCIAL MEDIA
We started by making tangram squares with papers with my grade 6 learners. Each learner had his or her own pieces. They discovered which shapes were the same. I asked them to make a square and a triangle from shapes A,G,C,E. They managed to do the shapes very fast.
First of all I thank this course in teaching us how to make our 7 pieces, it is easy and cheap. I did this in Grade 5, Grade 6 and Grade 7. They enjoyed the tangrams although it was not easy for them to do the shapes but it was very difficult for them to give-up. Others were saying:’No teacher this is impossible we cant make the shapes with this pieces’.
Many learners enjoy the tangrams, they did many shapes although there are those that are very difficult for them.
To clear up some confusion about what the word CONVEX means when we talk about convex polygons, imagine you are an ant crawling around the edges of a polygon. let’s say you are going around clockwise then, if you turn right at EVERY vertex until you get back to facing the way you set out from your starting point, then the polygon is convex and all the interior angles are less than 180 degrees. If you turned left at any vertex then that angle was greater than 180 degrees and the polygon was not convex.
This method also shows that the SUM OF THE EXTERIOR ANGLES OF ANY CONVEX POLYGON is 360 degrees because the ant must turn through a total of exactly 360 degrees on his way round.
If the polygon is REGULAR with n edges and vertices then each exterior angle will be 360/n degrees and each interior angle will be (180 – 360/n) degrees. For example the formulas give exterior angles of 72 degrees for n=5 and interior angles of 108 degrees.