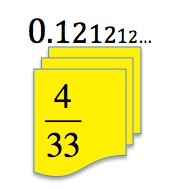Both these two numbers are recurring decimal fractions. The digits 12 are repeated again and again indefinitely.
0.12121212…
12.12121212…
Multiply the first number by 100. What do you get?
Subtract the smaller number from the bigger one. What do you get?
What does this tell you about the fraction in the picture \frac{4}{33}?
How could you check your result in a different way?
Now look at the two recurring decimals
0.44444…
4.44444…
Multiply the first number by 10. What do you get?
Subtract the smaller number from the bigger one. What do you get?
Can you use these two answers to find the common fraction that has the decimal equivalent 0.44444…?
Why do you think it was a good idea to multiply by 100 for the first fraction and to multiply by 10 for the second fraction?
Now match the following recurring decimals with their fraction equivalents.
| 0.151515… | \frac{7}{9} | 0.454545… | \frac{2}{3} | \frac{1}{7} | 0.777777… |
| \frac{26}{111} | 0.666666… | 0.14285714… | \frac{5}{33} | 0.234234… | \frac{4}{33} |
Click here for the REPETITION worksheet.
Click here for the Home Learning Guide.
Click here for Notes for Teachers.
Click here for the Repetition poster
If you enjoyed this article, please consider sharing it!
FOLLOW US ON SOCIAL MEDIA
