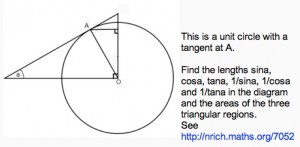This is a unit circle with a tangent at A.
The angle marked in the diagram is angle a.
Copy the diagram and find all the angles in terms of the angle a.
Find the six line segments in the diagram corresponding to sina, cosa, tana, 1/sina, 1/cosa and 1/tana.
Find the areas of the three triangular regions.
.See AIMSSEC Notes for Teachers.
This activity is adapted from the NRICH task Geometric Trig with permission of the University of Cambridge. All rights reserved.
If you enjoyed this article, please consider sharing it!
7 Responses to Geometric Trig
Leave a Reply
You must be logged in to post a comment.
FOLLOW US ON SOCIAL MEDIA
If you are doing trigonometry with Grade 11 this term then this problem makes a good activity. It is also a good revision activity for grade 12. There are notes and solutions to help the teachers.
Getting started
When you give a problem like this to your learners you don’t really know what is going to happen. If one or more of your learners has an idea then others can get started too but what tactics do we have if no-one can get started? Patricia realised that her learners didn’t understand the expression’unit circle’. So one thing to help get started is:
1) DISCUSS THE LANGUAGE
Underline the technical words in the problem and discuss
Unit circle tangent sina cosa tana triangular regions
e.g unit circle means a circle with radius 1 unit – mark on diagram
2) TRY A SIMPLER PROBLEM
If angle a = 50 degrees how many angles can you find? How many lengths of sides?
I hope your learners enjoy the problem
Christine
I taught trigonometry to grade 11 learners at the beginning of the term. We started by revising the trigonometric ratios and used the 2 unit triangle to derive the special values for angles 30 and 60. I encouraged them to get the values on their own without the use of the calcutor. Discovering on their own has helped them not to fear trigonometry. As this topic holds a lot of marks, good learners attitude will help them. I will share the activity with grade 12 teacher.
As we have already done the topic on trig in grade 11, I decided to give them this activity but it was difficult for them until I decided to give them a guide , we enjoyined the activity even though we took a longer time .I will give the grade 12 the same activity in term 3 as trig is done in term 3accoding to the pace setter
I gave this problem to my grade 12 learners,some were able to solve the problem without much guidance from the teacher whereas some needed some guiding and probing questions. They used the knowledge from analytic geometry, trigonometry as well as areas of both triangles and the circle, pythagoras theorem,etc. They enjoyed the problem and it helped them as they were preparing for the trial exams.
my grade 11 learners failed to understand and solve the problem on their own until a grade 12 learner gave them some hints about characteristics found on those drawings (circle, tangent and triangles) that is 90 degrees perpendicular, then they were able to attempt
I would use this task with my Grade 11 Learners when dealing with Analytical Geometry. With the Grade 12s I’d use it for revision especially in the third term, in preparation for the trial examination.