Currently viewing the tag: "Trigonometric equations"
This workshop reviews reduction formulae in terms of rotations and reflections. It offers learning activities that involve sorting and solving trigonometric equations and finding general solutions, or solutions within a
given domain, using known identities and graphical or unit circle representations. Suggestions are given organising group activies and learners presenting and explaining their ideas […]
Angles A, B and C are the angles of a triangle. Decide whether each of the following is an identity, always true for all triangles, or an equation, sometimes true. If you decide it is an equation find the solution or solutions and describe the corresponding triangle.
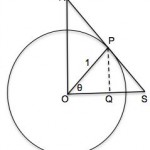
In the diagram the line OS is perpendicular to the lines OR and PQ.
The line RS is a tangent at P to the circle centre O and radius 1 unit.
Find the lengths OQ, PQ, PS, OS, OR and RP.
If OS and OR lie on the coordinate axes, what are the coordinates […]
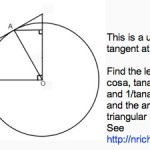
This is a unit circle with a tangent at A.
The angle marked in the diagram is angle a.
Copy the diagram and find all the angles in terms of the angle a.
Find the six line segments in the diagram corresponding to sina, cosa, tana, 1/sina, 1/cosa and 1/tana.
Find the areas of […]
FOLLOW US ON SOCIAL MEDIA
