Currently viewing the tag: "Theorem of Pythagoras"
What can you discover by accurately constructing some right angled triangles with integer edge lengths and their inscribed circles (incircles)?
If you make some conjectures, can you prove them?
Share ideas below about what you have discovered.
More ideas about incircles will be posted here. Watch this space.
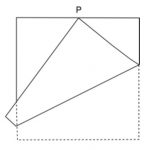
A square of paper 8 cm by 8 cm is folded so that the corner P coincides with the midpoint of an opposite edge as shown in the diagram.
Investigate the three triangles (where there is a single thickness of the paper) that are formed by folding in this way.
Click here for […]
There are hundreds of proofs of Pythagoras Theorem.
This diagram shows a proof.
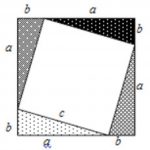
Look carefully. Can you see three squares?
Assuming that they are squares, can you prove that four of the triangles are congruent?
Can you now write down a proof of Pythagoras’ Theorem and explain the proof?
The second diagram […]
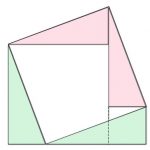
The right angled triangles numbered 1, 2, 3 and 4 in the diagrams all have sides of length a, b and c. They are identical (congruent) copies of each other.
Cut 4 congruent right angled triangles from some scrap paper. Arrange them as shown in diagram […]
This jigsaw has 7 pieces and 3 solutions with variations of those solutions.
You can download the template here and cut it out or make it on card. Try the puzzle yourself.
Either make a square with 5 pieces or make a square with 6 pieces.
The third challenge is to […]
Radio and TV stations broadcast from high towers. Their signals are picked up by radios and TV’s in houses within a certain radius. Because the Earth is spherical, these signals do not get picked up beyond the point of contact of the near horizontal tangent line as illustrated in the sketch.
What is the […]
STEP 1
1a) Double click on the picture above to start the movie showing how to draw a circle using the paperclip compass.
1b) Draw 2 circles of the same radius with centres A and B so that each circle goes through the centre of the […]
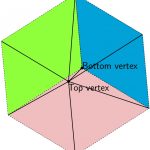
To make a model showing how cubes are made up of three square based pyramids, you will need a cardboard box, some string, some colouring pens and a knife or scissors to cut the box.
From one corner of a box cut squares all exactly the same size to form 3 faces of a cube, […]
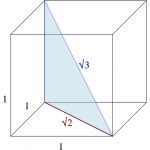
Copy this diagram. Why do the diagonals of a unit cube have lengths √2 and √3?
To draw a cube first draw a square, then draw another square the same size that looks as if it is behind the first square, then join the vertices with four parallel lines.
What are the lengths […]
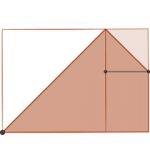
Take a sheet of A4 paper. First fold the top left corner to meet the bottom edge and press the fold flat. Then fold the top right corner to meet the edge that you folded down.
Can you prove that the quadrilateral you have made is a kite?
Can you find the perimeter of the […]
FOLLOW US ON SOCIAL MEDIA
