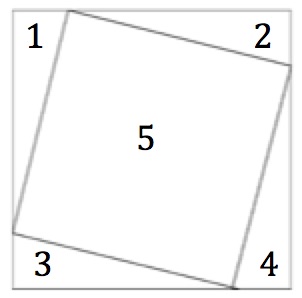
The right angled triangles numbered 1, 2, 3 and 4 in the diagrams all have sides of length a, b and c. They are identical (congruent) copies of each other.
- Cut 4 congruent right angled triangles from some scrap paper.
- Arrange them as shown in diagram 1 in your notebook.
- What do you notice about the quadrilateral labelled 5?
- Draw the square frame that this arrangement fits into exactly.
- How can you be sure that the frame is a square?
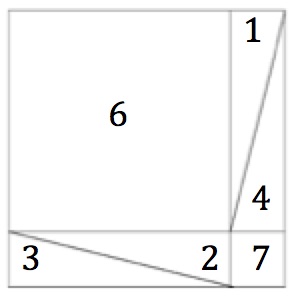
- Place the 4 triangles inside the square frame as in diagram 2.
- What do you notice about the quadrilateral labelled 6 and 7?
- What can you deduce about the areas of quadrilaterals 5, 6 & 7.
- Does the same hold for any 4 congruent right angled triangles?
- What have you proved?
These 4 congruent triangles are arranged in the squares shown in the diagrams all of which have sides (a + b).
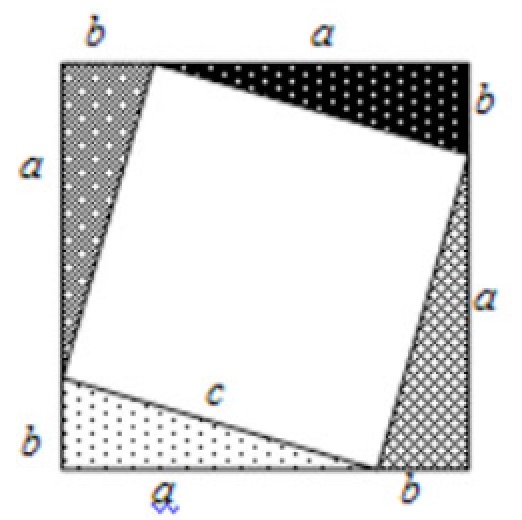Think about the areas in the diagrams.
Just take away the four identical right angled triangles from each of the diagrams. What is left?
How can you be sure that the shapes labelled 5, 6 and 7 are squares?
What does this tell you about the area of square 5 compared with the areas of squares 6 and 7?
Click here for the PYTHAGORAS JIGSAW worksheet.
Click here to watch the GTEN workshop for primary and secondary teachers all about how learners can discover Pythagoras Theorem for themselves.
Click here for the PYTHAGORAS JIGSAW Inclusion and Home Learning Guide
Click here for Notes for Teachers.
Can you also use the diagram showing shapes 1, 2, 3, 4, 6 and 7 to show that
(a + b)^2 = a^2 + b^2 + 2ab?
If you enjoyed this article, please consider sharing it!
FOLLOW US ON SOCIAL MEDIA
