30-minute Fractals Lesson and Follow Up
 Start by watching the video https://youtu.be/B2dkNPaTmDY
Start by watching the video https://youtu.be/B2dkNPaTmDY
 Each student should have a stage 3 Sierpinski triangle of edge length about 6.5 cm and a colouring pen, and should colour their triangle as shown by the black filling in the small diagram.
Each student should have a stage 3 Sierpinski triangle of edge length about 6.5 cm and a colouring pen, and should colour their triangle as shown by the black filling in the small diagram.
The class will make poster of a stage 6 Sierpinski triangle using 27 of the triangles that the students have coloured in. You can see how, at each stage, 3 triangles are used to make up the Sierpinski triangle at the next stage.
But you have to imagine shrinking the triangles back to the stage 0 size each time.
 This fractal is the result of repeating the same process infinitely often. The triangles in our poster just help us to understand the structure of the fractal. Imagine the process going on for ever making more and more and more triangular holes in the gasket.
This fractal is the result of repeating the same process infinitely often. The triangles in our poster just help us to understand the structure of the fractal. Imagine the process going on for ever making more and more and more triangular holes in the gasket.
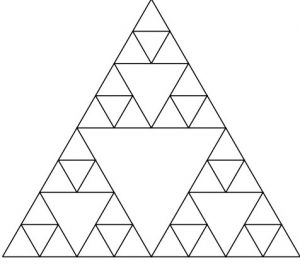
 Here is a poster made by a class of a stage 6 Sierpinski triangle.
Here is a poster made by a class of a stage 6 Sierpinski triangle.
If you want to extend the 30-minute lesson, and if you have enough time and space, if you have a big class, or if several classes combine their efforts, you might make a stage 7 poster with 81 triangles or even a stage 8 poster with 243 triangles.
Click here for a single PDF with links to all the GML19 Resources for Learning and Teaching about Fractals as given in the list of links below.
NOTES FOR TEACHERS OF DIFFERENT AGE GROUPS
 Click here for the Sierpinski Triangle poster
Click here for the Sierpinski Triangle poster
Click here for slides of the FRACTALS video
Click here for a version of the video for teachers https://youtu.be/BYsNxHls3P4
Click here for Notes for Teachers of Upper Primary and Secondary students.
Click here for Notes for Teachers of Lower Primary and Support for Special Needs
Click here for Notes for Teachers of Early Years
Click here for a Short Explanation of the History of Fractals
MORE FRACTALS RESOURCES TO DOWNLOAD
Ages 5 to 7
Comparing Pyramids for young learners
Counting, Colours and Triangles for young learners
Ages 7 to 11
 Global Maths Lesson – The World We Share – Bar charts
Global Maths Lesson – The World We Share – Bar charts
Make a von Koch Fractal Poster
Pascal’s Triangle – Number and Fractal Patterns – Multiples
Make a Sierpinski Tetrahedron with toothpicks or newspaper sticks
Make a Christmas Sierpinski Tetrahedron Tree
Ages 11 to 16
Global Maths Lesson – The World We Share – Bar charts
Global Maths Lesson – The World We Share – Pie charts
Pascal’s Triangle – Number and Fractal Patterns – Multiples
Make a von Koch Fractal Poster
Sierpinski Triangle – follow-up questions and answers on Number Patterns, Lengths, Areas and Fractions
Sierpinski Tetrahedron – Number and Shape Patterns
Make a Sierpinski Tetrahedron with toothpicks or newspaper sticks
Make a Christmas Sierpinski Tetrahedron Tree
Order to Randomness Download a free booklet giving projects on Visualising Graphs, Really Long Curves, Reasoning and Proof, The Mandelbrot Set, Chaos
Ages 16+
Global Maths Lesson – The World We Share – Pie charts
Pascal’s Triangle – Number and Fractal Patterns – Multiples and the Binomial Theorem
Sierpinski Triangle – follow-up questions and answers on Number Patterns, Lengths, Areas and Fractions
Sierpinski Tetrahedron – Number and Shape Patterns
The von Koch Curve – sequences and sums of geometric series
Click here for a video on Fractal Dimension
Click here for an explanation of Fractal Dimension.
South Africa COVID-19 News
Here is the official website for COVID-19 updates.
Login
SUPPORT AIMSSEC





