Pascal’s Triangle and Fractal Patterns
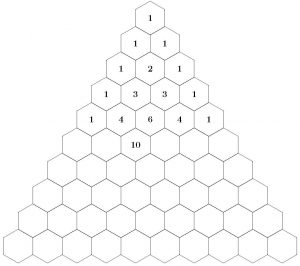 Can you see what the rule is for filling numbers in the hexagons? Continue the pattern using the same rule. If you get it right the bottom row will start 1, 9, 36, 84, …
Can you see what the rule is for filling numbers in the hexagons? Continue the pattern using the same rule. If you get it right the bottom row will start 1, 9, 36, 84, …
Shade the hexagons where the number inside is odd all in one colour. Using a contrasting colour, shade the hexagons where the number inside is even. What do you see?
Can you see a way to do this without having to do any arithmetic?
Download a large grid with 21 rows. Fill in the Pascal’s triangle pattern of numbers in this grid as a class project. Shade the odd numbers. What do you notice about the pattern of colours?
On another 21 row grid colour in all the multiples of 3. Repeat on other grids, colouring the multiples of 5, then 7, then 9, …
What do you notice? Where have you seen these patterns before?
What happens if you look at multiples of 2, 4, … ?
Although this triangle, and the patterns associated with it, were known long before Pascal’s time, it is called Pascal’s triangle. It is very important in algebra and probability theory so it’s useful to get to know it’s properties. You may see nCr on one of the buttons on your calculator; this gives the numbers on Pascal’s triangle.
Click here for a short historical note.
Click here for the PASCAL’S TRIANGLE AND FRACTAL PATTERNS worksheet
Click here for the Notes for Teachers.
South Africa COVID-19 News
Here is the official website for COVID-19 updates.
Login
SUPPORT AIMSSEC





