NUMBER TRICK This is for secondary students and top primary. On any calendar of any month of any year put a box around four dates, two in one week and two in the following week (all four dates must be within the same month). Add the numbers up and tell me the total. I can […]
The FIFTEEN GAME is a game for two players (or a class split into two teams).
Take it in turns to choose one of the numbers 1 to 9. It is now your number and your opponent cannot choose it. Each number can be chosen only once.
To win, be the first to pick 3 […]
Find a cuboid (with edges of integer values) that has a surface area of exactly 100 square units.
Is there more than one?
It is quite easy to find a few solutions. The big challenge is to find all possible solutions.
Can you provide a convincing argument that you have found […]
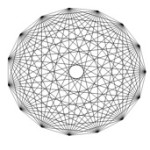
What can you see in this diagram?
Could you draw it? Could you draw a similar diagram with just 5 or 6 points around the outside? Try it?
How many lines are there in your diagrams? How many lines are there in the original diagram? Can you find a way of working out […]
Five red-eye frogs and five orange frogs line up in a row with a space between them.
They have to change places but they can only hop, one frog over another frog or slide to an empty space next to them.
Red-eye frogs can […]
Suppose you have two 1s, two 2s and two 3s.
Arrange these six digits in a list so that:
between the two 1s there is one digit giving 1?1,
between the two 2s there are two digits giving 2??2,
between the two 3s there are three digits giving 3???3.
[…]
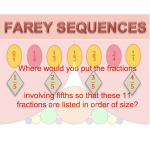
It is not difficult to put a list of decimals in order of size. But what about ordering fractions?
John Farey introduced sequences of sequences of fractions in order of size, now called Farey sequences. Can you discover his method from the following examples?
What patterns do you see in them?
Suppose you have to share 9872 gold coins between 8 people.
You give the coins out in thousands until there are less than 8000 left.
Then you give out one hundred at a time until there are less than 800, then […]
Ram had 15 coins, all the same kind, and he put them into 4 bags.
He labelled each bag with the number of coins inside it.
He could then pay any sum of money from 1 coin to 15 coins using one or more of the bags without opening any of the bags.
How […]
South Africa COVID-19 News
Here is the official website for COVID-19 updates.
Login
SUPPORT AIMSSEC