The von Koch Curve

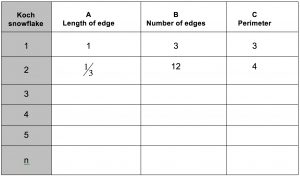
Image starting with an equilateral triangle and replacing each edge by a zig-zag curve made up of 4 pieces. Each of the 4 pieces is one third of the length of the line segment it replaces so it looks as if equilateral triangles have been attached to the shape. Now imagine repeating this process over and over again. What would happen? The edges of the triangle at the first stage are one unit in length. Here are the first four stages.

The Koch curve is sometimes called the snowflake curve. This curve is the outer perimeter of the shape formed by the outer edges when the process is repeated infinitely often.

1. The table shows that the snowflake construction produces three types of sequences A, B and C. The last row gives the nth term in the sequence. Describe the type of sequence in each case giving two properties of the sequence.

2. What happens to the perimeter as n tends to infinity?

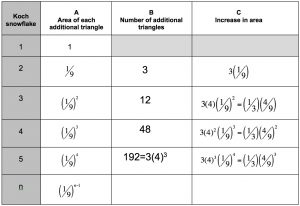
The next table shows some of the calculations of the area enclosed by the Koch curve.

3. Show that the sum of the increases in area in column C is

Find the sum of this series.

In studying what happens to the area inside the curve in this iteration it is convenient to take the area of the original triangle as 1 square unit for the next calculations. To relate this calculation to the previous table where the edge of the triangle has length 1 unit use the scale factor \frac{\sqrt{3}}{4} .

Investigate the increase in area of the Von Koch snowflake at successive stages. Call the area of the original triangle one unit and complete the table below.

4. What happens to the sum of the increases in area as n tends to infinity?

5. The difference between what happens to the perimeter and to the area of the Koch snowflake curve as n tends to infinity is very interesting. Comment on this difference.

Click here for Notes for Teachers