Odds and Colours Games
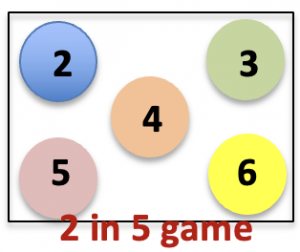 Place in a bag or envelope two balls (or cards) with odd numbers on them, and 3 with even numbers, and play the 2 Odds in 5 game, for example with balls numbered 2, 3, 4, 5 and 6. Pick out two balls or cards at random without replacing the first one. Replace them both before the next draw. If the total is odd you win a point, if it is even you lose and your opponent gets a point. Are you equally likely to win or to lose (is it a fair game)? The first player to score 5 points wins the game.
Place in a bag or envelope two balls (or cards) with odd numbers on them, and 3 with even numbers, and play the 2 Odds in 5 game, for example with balls numbered 2, 3, 4, 5 and 6. Pick out two balls or cards at random without replacing the first one. Replace them both before the next draw. If the total is odd you win a point, if it is even you lose and your opponent gets a point. Are you equally likely to win or to lose (is it a fair game)? The first player to score 5 points wins the game.
Also play the 3 games shown below, the rules are the same. Using number cards do your own experiments to find out what combinations of numbers give fair games. Which set of balls would you choose to give yourself the best chance of winning? 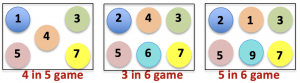
Can you find a different set of numbers to make this a fair game? 
Put in a bag 3 and 6 blue objects, identical in all respects except colour. Each player must choose whether to to be a ‘same’ player who wins when the 2 objects drawn are the same colour, or a ‘different’ player who wins when they are different. Take turns to pick two objects at random, first one then another without replacing the first one, and score a point (or not) depending on whether the obs jects are the same colour. Put the objects back and shake the bag. Repeat until one of the players has won 5 points.
Is this a fair game? Would it still be a fair game if you put different numbers of coloured objects in the bag? Put 5 red and 5 blue in a bag and play the game? Is this a fair game? Keep a record of all your results and investigate what proportion of each type of object makes it a fair game.
What do you notice about the Odds games and the Red Blue games?
Click here for the ODDS GAMES worksheet.
Click here for the PRIMARY ODDS GAMES Inclusion and Home Learning Guide.
Click here for the SECONDARY ODDS GAMES Inclusion and Home Learning Guide.
Click here for Notes for Teachers for years 9 to 11.
Click here for Proof Sorting Activity for Years 12 & 13
This problem is adapted from the NRICH task Odds and Evens with permission of the University of Cambridge. All rights reserved. You can play the games using the NRICH interactive computer simulations.
South Africa COVID-19 News
Here is the official website for COVID-19 updates.
Login
SUPPORT AIMSSEC





