Currently viewing the tag: "Triangles"
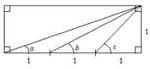
This rectangle measures three units by one unit.
The diagram shows three angles a, b and c.
How many ways can you prove that a + b = c?
What other interesting properties can you find?
When this activity was originally published on NRICH, two boys from Madras School in St Andrew’s, Scotland sent […]
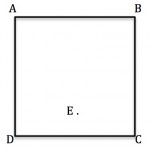
The point E is inside the square ABCD and AEB is an equilateral triangle. Find the angles EBC, BEC and ECD and give reasons for your answers.
Click for Teacher-Notes-GEO-PROB.
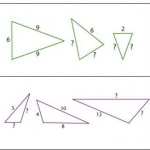
Each picture shows 3 similar triangles.
They are called similar because they are the same shape, they have the same angles and the lengths of the edges are in the same ratio. For example in this diagram the edges in each triangle are all in the ratio 2 : 3 : 4 […]
Two flagpoles are 30 metres apart. One has height 10 m and the other has height 15 m. Two tight ropes connect the top of each pole to the foot of the other.
How high do the two ropes intersect above the ground?
How many different methods can you find to solve this problem?
What […]
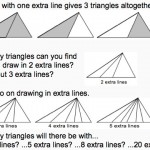
Click here to download the COUNTING TRIANGLES worksheet.
Click here for the Notes for Teachers.
Click here to download the COUNTING TRIANGLES poster
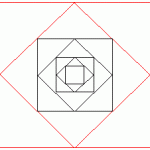
Seven squares are drawn inside each other. The centre points of each side of the outer square are joined to make a smaller square inside it and so on.
The centre square has the area of 1 (one) square unit.
Draw the diagram. You can download square dotty paper here.
What is […]
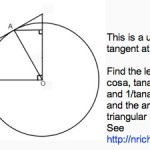
This is a unit circle with a tangent at A.
The angle marked in the diagram is angle a.
Copy the diagram and find all the angles in terms of the angle a.
Find the six line segments in the diagram corresponding to sina, cosa, tana, 1/sina, 1/cosa and 1/tana.
Find the areas of […]
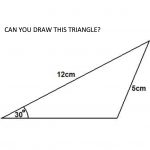
Imagine you have a pencil, ruler, protractor and compass and you try to draw this triangle. Is it possible?
If you have geometry instruments then try it for yourself. What do you notice?
Can you give reasons for your answer to the question “Is it possible?”
Click here for The Notes for Teachers. […]
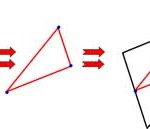
You are only given the three midpoints of the sides of a triangle.
How can you construct the original triangle?
Is there more than one way to find the answer?
What similarities and differences can you see between this Triangle Midpoints problem, The Checkit Game with Addition https://aiminghigh.aimssec.ac.za/checkit-game/ and Polycircles https://aiminghigh.aimssec.ac.za/polycircles/
If you take the edge length of the equilateral triangles in this picture as the unit for length, what would be the exact size of the hole ?
Alternatively, if the area of an equilateral triangles is taken as the unit for area, what size is the hole?
Click here for Notes for […]
FOLLOW US ON SOCIAL MEDIA
