Currently viewing the tag: "Similarity"
See the Bendy Quads video https://bit.ly/BendyQuadsVideo
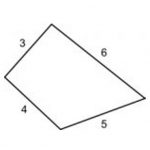
Four rods are hinged at their ends to form a convex quadrilateral with edges of length 3, 4, 5 and 6 (in that order). Investigate the different shapes that the quadrilateral can take if the polygon is always convex.
How do the angles change […]
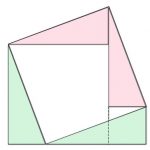
There are hundreds of proofs of Pythagoras Theorem.
This diagram shows a proof.
Look carefully. Can you see three squares?
Assuming that they are squares, can you prove that four of the triangles are congruent?
Can you now write down a proof of Pythagoras’ Theorem and explain the proof?
The second diagram […]
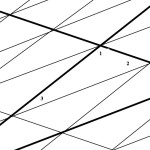
This diagram shows 3 sets of parallel lines. What do you notice in the diagram?
Look at the triangle with angles marked 1, 2 and 3.
Call this T.
Label angles equal to these angles. Why are they equal?
Look at the larger heavily outlined triangle.
How many copies of triangle T can […]
Investigations of angle properties of parallel lines, similarity in 2 and 3 dimensions and scale factors for linear, area and volume enlargement.
Click here to download a pdf with all you need to run your own professional development workshop.
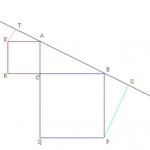
In the diagram ASRC and BCQP are squares and PU and ST are perpendicular to the straight line TABU.
Prove that PU + ST = AB.
These ‘trisquares’ are made up of three squares and each has an area of 3 square units.
Can you fit them together to make an enlargement of the shape? What is its area?
Can you fit trisquares together to make enlargements of scale factors 3, 4 and 5? What are their areas?
Is it […]
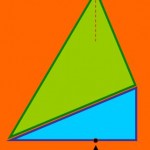
Two right-angled triangles are joined as shown in the diagram.
The green triangle has side lengths of 65, 52 and 39 cm and the blue triangle has side lengths of 52, 48 and 20 cm.
An object is dropped vertically from the top of the green triangle hitting the base by […]
FOLLOW US ON SOCIAL MEDIA
