Currently viewing the tag: "Polygons"
Find some sticks, they could be twigs, or matchsticks or cocktail sticks, or rolled paper sticks, or pasta like spaghetti broken into short lengths, but they must all be the same length.
Arrange 16 sticks into this pattern.
As an easy starter, can you remove 4 sticks and leave […]
Squares 1, 2 and 3 all have edges of length 1 unit.
The top edge of square 2 is split into equal parts of length ½.
The left hand edge of square 3 is split into equal parts of length ½.
The top and bottom edges of square 3 is split into lengths ¼, […]
INDIVIDUAL OR WHOLE CLASS ACTIVITY
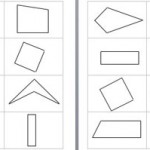
Sort these quadrilaterals into 4 sets of 4 and describe the properties of each set.
.GROUP ACTIVITY – groups of 4
Cut out 16 cards and mix them up.
Give each member of the group 4 cards. They must give their cards to other members of the […]
How many right-angled triangles of different sizes can you make by joining the dots on the 5 by 5 spotty grid?
Describe your triangles and say what geometrical properties they have.
You can download […]
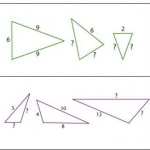
Each picture shows 3 similar triangles.
They are called similar because they are the same shape, they have the same angles and the lengths of the edges are in the same ratio. For example in this diagram the edges in each triangle are all in the ratio 2 : 3 : 4 […]
Draw chords to cut a regular hexagon
(a) into two pieces which, when put together, make a parallelogram;
(b) into three pieces which, when put together, make a rhombus;
(c) into four pieces which, when put together, make two equilateral triangles.
(d) What angles can you find in each of your shapes?
(e) If […]
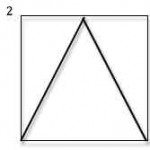
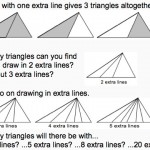
Click here to download the COUNTING TRIANGLES worksheet.
Click here for the Notes for Teachers.
Click here to download the COUNTING TRIANGLES poster
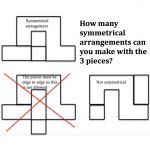
In how many ways can you fit all three pieces together, edge to edge, to make shapes with line symmetry?
The first of these examples shows a symmetrical arrangement, the second is not allowed because the pieces are not placed edge to edge and the third is not symmetrical.
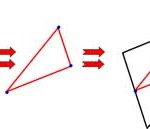
You are only given the three midpoints of the sides of a triangle.
How can you construct the original triangle?
Is there more than one way to find the answer?
What similarities and differences can you see between this Triangle Midpoints problem, The Checkit Game with Addition https://aiminghigh.aimssec.ac.za/checkit-game/ and Polycircles https://aiminghigh.aimssec.ac.za/polycircles/
FOLLOW US ON SOCIAL MEDIA
