Farey Sequences
It is not difficult to put a list of decimals in order of size. But what about ordering fractions?
John Farey introduced sequences of sequences of fractions in order of size, now called Farey sequences. Can you discover his method from the following examples?
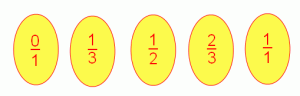 The third Farey sequence shown here lists in order, in their simplest form, all the fractions between 0 and 1 that have denominators 1, 2 and 3.
The third Farey sequence shown here lists in order, in their simplest form, all the fractions between 0 and 1 that have denominators 1, 2 and 3.
 The fourth Farey sequence shown here lists in order, in their simplest form, all the fractions between 0 and 1 which have denominators 1, 2, 3 and 4.
The fourth Farey sequence shown here lists in order, in their simplest form, all the fractions between 0 and 1 which have denominators 1, 2, 3 and 4.
Can you find the fifth Farey sequence? What about sixth Farey sequence and more sequences in this sequence of sequences?
What do you notice about these sequences?
Click here to download the FAREY SEQUENCES worksheet.
Click here to download the Notes for Teachers.
As follow up work see:
Mediant Madness https://nrich.maths.org/831
Ford Circles https://nrich.maths.org/6594
Farey Neighbours https://nrich.maths.org/6598
This problem is adapted from the NRICH task of the same name with permission of the University of Cambridge. All rights reserved. Also see related problems on NRICH.
South Africa COVID-19 News
Here is the official website for COVID-19 updates.
Login
SUPPORT AIMSSEC





