Graphing Quadratic Equations
Graph $y={ x }^{ 2 }-2x-1$ .
1. What type of an equation is this?
2. Remember the general form of an equation of this nature: $y={a x }^{ 2 }-bx-c$
When $a > 0$ the graph is $\cup$ shaped and when $a < 0$ it is $\cap$ shaped. What is the situation in our problem?
3. Does the graph of $y={ x }^{ 2 }-2x-1$ intersect with the x-axis? What is the value of y when this graph crosses the x-axis? Can you solve ${ x }^{ 2 }-2x-1=0$ ?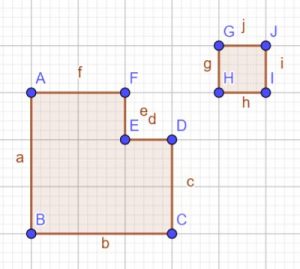
Think of the method of completing a square for solving quadratics. Geometrically, you are thinking of adding shape GHIJ to the bigger shape to make it a complete square, then solve the problem. What are the two values of $x$ which are solutions to ${ x }^{ 2 }-2x-1=0$?
4. From ${ x }^{ 2 }-2x-1 = {(x – 1)}^{2} – 2 = 0$, notice that the graph is above the x-axis for ${(x – 1)}^{2}\ge 0$ for all values of $x$. $\therefore$ The minimum value of ${(x – 1)}^{2}$ is zero and this happens when $x – 1 = 0$ $\rightarrow$ $x = 1$. What is the value of y when $x = 1$? Comment on this point.
5. Parabolas are symmetrical shapes, what is the line of symmetry of this graph?
6. At what point(s) does the graph cross the $x$- axis?
7. Taking into consideration (accommodating) all the special points you have obtained so far, draw a Cartesian plane. Plot all the special points. Graph $y={ x }^{ 2 }-2x-1$.
Click here to download the GRAPHING QUADRATICS poster.
Click here to download the GRAPHING QUADRATICS worksheet.
Click here for Notes for Teachers.
South Africa COVID-19 News
Here is the official website for COVID-19 updates.
Login
SUPPORT AIMSSEC





