What is the rule (or fu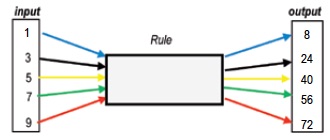
nction) that gives the outputs corresponding to the inputs shown in the diagram mapping 1 to 8 and 3 to 24 etc?
The Function Game is played in silence. Learners have to guess the function in the teacher’s mind. The teacher tells the learners that she wants them to tell her what she is doing. She asks the learners to give her numbers and writes them on the board in a column with the outputs for the functions rule she is thinking of alongside. She asks “What am I doing?”. A learner who thinks he or she has guessed what the teacher is doing puts up a hand and the teacher suggests a number and asks the learner to do the same with it and give the answer. If the learner gets the right output the teacher congratulates him and writes it on the board. The game continues until most of the learners have guessed the rule. Then learners who have guessed it explain what the teacher was doing for the benefit of those who did not guess it and the game is repeated with another rule.
For example if the function is x \to 3x + 5 then 2 \to 11 , 3 \to 14 , 10 \to 35 etc.
The game can be varied by sometimes using the numbers suggested by learners as inputs and sometimes as outputs, the teacher writing the numbers in the appropriate input and output columns. This can lead to a class discussion of inverse functions. For example, if the output is 41 for the function x \to 3x + 5 how do you find the input? The inverse function is x \to \frac{x - 5}{3} so the input is 12.
Click here for the FUNCTION GAME poster.
Click here for the FUNCTION GAME worksheet.
Click here to download the FUNCTION GAME Inclusion and Home Learning Guide.
Click here for the Notes for Teachers.
If you enjoyed this article, please consider sharing it!
FOLLOW US ON SOCIAL MEDIA
