Tops

For your company, you have to design spinning tops made from two pieces glued together, a hemisphere and a cone, and you have to plan how they will be manufactured, packaged and sold.

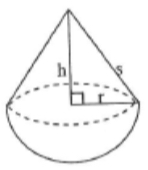
(1) The radius of the circular surface where the pieces are glued together is 3 cm. The slant height of the cone is 5 cm. Work out the total volume and surface area of the spinning top (top A).

(2) Each top is packed in a box measuring 6.5 cm by 6.5 cm by 7.5 cm. How many tops will fit into a packing case measuring 55 cm by 55 cm by 55 cm?

(3) You investigate other designs for two more tops, made the same way with the circular surface where the pieces are glued together having radius 3 cm. For top B the volume of the hemisphere is equal to the volume of the cone and for top C the surface area of the hemisphere is the same as the surface area of the cone. Find h cm, the height of the cones for top B and for top C.

(4) Make your own cone, and a cylinder the same height, using the templates in the worksheet, from paper or scrap card or plastic.  Fill the cone with sand, lentils, rice or something similar and investigate the relationship between the volume of the cone and the volume of the cylinder.  This is not a proof of the formula for the volume of the cone but you will need to learn integral calculus to prove the formula.

(5) Work out the dimensions of a cuboid with the same volume as the cylinder and with the same height as the cylinder and cone.

Click here for the TOPS Inclusion and Home Learning Guide.

Click here for the TOPS worksheet.

Click here for the Notes for Teachers