Difference of Squares and Area
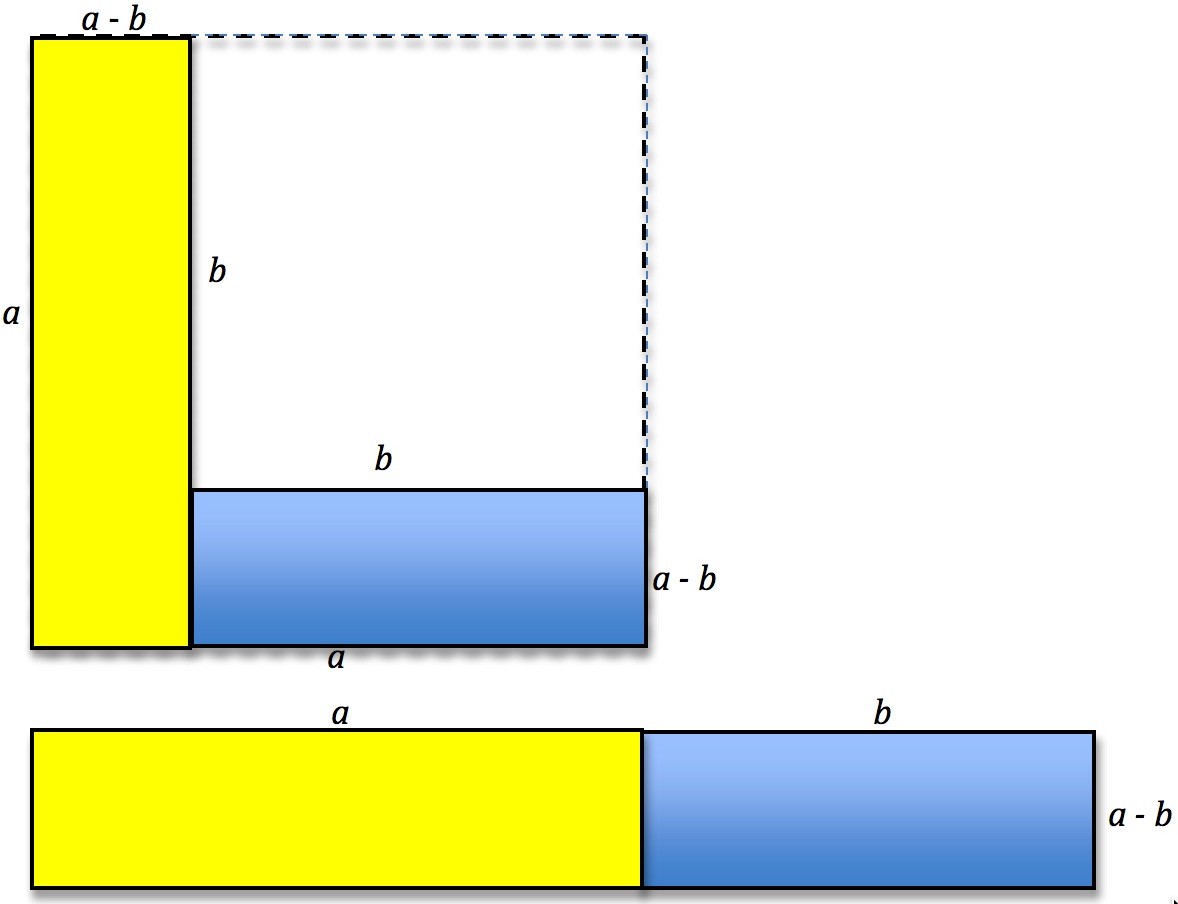 What do you see in this image?
What do you see in this image?
What is the area of the bigger square edged by dotted line segments of length a?
What is left of that area if you take away a square with edges of length b?
What is the area of the rectangle formed by the yellow and blue rectangles placed end to end?
What can you deduce from this?
Click here to download the DIFFERENCE OF SQUARES AND AREA worksheet.
Click here for Notes for Teachers.
Click here for the DIFFERENCE OF SQUARES AND AREA poster
South Africa COVID-19 News
Here is the official website for COVID-19 updates.
Login
SUPPORT AIMSSEC





