Fibonacci (in the year 1202) investigated a problem about how fast a population of rabbits would grow in the following circumstances, starting with just one pair of rabbits:
Suppose a newly-born pair of rabbits, one male, one female, are put in a field. Rabbits are able to mate at the age of one month so that at the end of its second month a female can produce another pair of rabbits.
Suppose that our rabbits never die and that the female always produces one new pair (one male, one female) every month from the second month on.
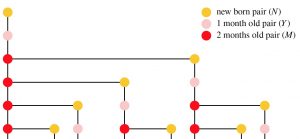
Use the diagram to find out how many pairs of rabbits there will be in one year and so to solve the problem?
The diagram shows the population of rabbits at times t = 0, 1, 2, 3, 4 and 5 months.
At time t = 0 the original pair of new-born rabbits are shown by a yellow disc.
At time t = 1 month the same pair are shown in pink, as young rabbits.
At time t = 2 months the diagram shows the same rabbits (now mature) in red together with a pair of new-borns (in yellow).
At time t = 3 months the original pair have produced a 2nd pair of new-borns and their 1st pair are now young and shown in pink.
The population is also shown at times t = 4 and 5 months.
Extend the tree diagram to show the population at t = 6 months.
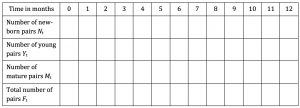
Fill in the table for times t = 0 to t = 6 months.
Write down formulae for Nt, Yt, Mt and Ft and explain why the pattern will continue month after month.
In 1202 Leonardo of Pisa, who is now known as Fibonacci, published a ground-breaking book called ‘The Book of Calculation’ (Liber Abaci in Latin) which included this problem. Fibonacci had travelled in Asia as a merchant and he brought from India to Europe a new way of writing numbers – the Hindu-Arabic Numeral system. His methods influenced the development of mathematics in Europe and provided merchants with efficient ways to record commercial transactions.
Henry E Dudeney (1857 – 1930), an Englishman famous for his puzzles, adapted Fibonacci’s Rabbits problem. He changed months into years, and rabbits into bulls (male) and cows (females) and stated the problem as follows:
If cows produce their first she-calf at age 2 years, and after that another she-calf every year, how many she-calves are there after 12 years, assuming that none die?
Explain the solution to this problem.
Click here for the FIBONACCI’S RABBITS worksheet
Click here for the FIBONACCI’S RABBITS Notes for teachers
If you enjoyed this article, please consider sharing it!
FOLLOW US ON SOCIAL MEDIA
