Coordinate Patterns
I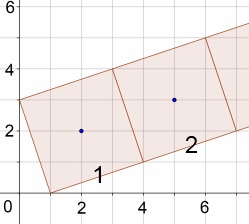 magine this pattern of squares continuing on and on …
magine this pattern of squares continuing on and on …
How do you find the coordinates of the centre of square 1 if you know that (0, 3), (3, 4), (4, 1) and (1, 0) are vertices?
What are the coordinates of the centre of the 20th square?
Imagine the sequence of squares extending to the left … -2, -1, 0, 1, 2, 3, …
Can you explain why the centre of square -1 is (-4 ; 0)? What are the coordinates of the centre of square number -10?
Explain how you can find the coordinates of the vertices of square 2?
Now the big challenge: explain how you can find the coordinates of the vertices of square n?
Click here to download the COORDINATE PATTERNS worksheet.
Click here to download Notes for Teachers.
The ideas for this problem originally came from the SMP11-16 booklets on Coordinate Patterns published by CUP.
22 Responses to Coordinate Patterns
Leave a Reply Cancel reply
You must be logged in to post a comment.
South Africa COVID-19 News
Here is the official website for COVID-19 updates.
Login
SUPPORT AIMSSEC






this was a lovely exercise reviving the pattern knowledge
I think this would be a good activity to give to the learners to do in the beginning of a patterns lesson,but it requires that they are already familiar with the co-ordinate geometry as well as transformation geometry.
to use figures or something that learners see during a lesson helps them to understand more easily
The learners would be aware of what coordinates are and what a pattern is.there may be a need to revise number systems with a special focus on integers.
I would let the learners work in pairs and ask them to…
1. Write down coordinates of square centres 2 to 4.
2. Tell if they see any pattern with the x-coordinates as one goes up.
3. Tell if they see any pattern with the y-coordinates as you goes up.
Then,I would ask different pairs to write coordinates for further square centres.
Now that sounds like there’s some proportion there,is it direct or indirect?
To use this type of activity,prior knowledge of co-ordinates is going to be vital.This might mean u will have to give them an activity to determine how much they know before u give them this one.Remember even at grade 12 level learners are still faced with the challenges of lack of the basic mathematical knowledge.
But I think if your lesson is about Number patterns,this activity will also serve that purpose of assessing the baseline knowledge of co-ordinate as well as transformational geometry
May you kindly share the steps involved in trying to find the co-ordinates of that 20th square without having to write down all the co-ordinates
I would decide on the topic and its objectives for that particular period. Topic : Coordinates – Objectives : identify x and y coordinates.
Prior knowledge : Patterns, Cartesian plane
Activity : On patterns, identification of coordinates on the cartesian plane.
The challenge with problem 2 is counting to the left coming with negative pattern. Learners are used to counting terms starting from one. The learners might not know that negative is just a direction. The prior knowledge must be on direction and a link with physical sciences.
Much time should be spent on focusing on a direction.
I think that will need the revisiting of the numbers system as it incorporates the negative numbers in an integer set so I don’t think it will be such a challenge
This is a good activity to get students thinking about quite a lot of things combined. Squares, coordinates,patterns and gradients.
This is a beautiful way of introducing learners to patterns. In this problem the learners prior knowledge of coordinates are revised. The learners will be faced with two types of patterns, the x and the y values. After identifying the general term for both the x and the y value, the learners should be able to solve the problems.
The learners will have problems in identifying with negative terms(where eg. this is the -3rd term) as we teach learners that the number of terms cannot be negative.
prio knowledge is important and intergration of sequence and coordinate(x;y) is required to this problem therefore it is interesting, challenging and requires a critical thinking to learners
One way of looking at this problem is by finding the defining equation of all the points that are in the centers of theses squares. then one can find the the center of the 20-th square.
quite a good problem!!!!
1. Explain to the learners the topic, objectives, and evaluation.
2. Allow learners to represent the squares on their geoboards in both directions, i.e. right and left. (if geoboards are not big enough, they can use square dot papers for the same exercise.
3. Allow learners to write coordinate corresponding to the x-valuse on the Cartesian plane.
3. Let them discuss the relationship they observe, when going towards the right, or moving to the left, and the same for up and down.
4. Ask them to find the correct coordinates using their discovered rule, after analysing their own squares.
5. Explain to them that since when we talk of terms, we always refer to counting numbers, going to the left simply means counting too, but in the opposite direction.
6. I would then allow them to experiment using their self-created squares.
Mandla i think by also letting them calculate the common difference in both x and y-values and then use the formula to generate the coordinates
This activity encourages students to visualize arithmetic sequences in a more simpler and practical way.
This activity is a good example of integration sections with the subject content because it integrate coordinate geometry and number patterns in one lesson.
1) Ask your learners to determine the coordinate of the center of any square from the given sequence of squares, at first.
2)Ask them to determine the coordinates of the vertices of the square they managed to determine the center from number 1.
3) Use analytically method to determine the midpoint.
4) Use the know of number pattern to determine the term number 18 if the squares are placed in the same order continually.
The learners must do the activity using their logical thinking skills.
Prior knowledge must be taken into consideration.
The learners must know the x-axis and y-axis.
The learners must look first term and constant difference and lastly they formulate the rule
In this activity learners need to have a good understanding of how to plot the points in a Cartesian plane as well as to be able to see the scale of the grid.I think learners if they can generate the formula to work this, will be of great advantage to them so that they will be able to calculate the co ordinates of the centre of any number of terms.But there is still a problem with the learners, are not motivated when they do their work if I can have an idea of how to motivate the learners I think that will be of great appreciation from my side.
i enjoyed learning about this number pattern .I never thought of before I had only examples taken from Algebra.
Hi Dr Toni I gave this activity to my learners.Some recognised da pattern but others failed.What I have noticed with negative numbers is that learners start to panic when they see them they become demotivated so what I have done is to give them more activities based on neg numbers to gain back their confidence. Thanks Toni