Currently viewing the category:
"Lesson Activities"
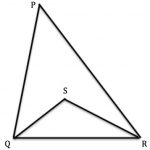
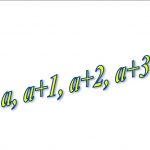Investigate different triangles PQR where the angle QPR is 40 degrees. Choose your own angles at Q and R, for example someone might choose 90 degrees and 50 degrees and someone else 62 degrees and 78 degrees.
Accurately draw the internal bisectors of the angles at Q and R to meet […]
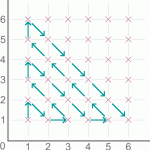
Look at the route the arrows follow in this diagram. Look away from the screen and try to describe their path.
Will the route pass through the point (18,17)?
If so, which point will be visited next? Explain how you found out.
How many points does the route pass through […]
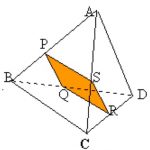
ABCD is a regular tetrahedron and the points P, Q, R and S
are the midpoints of the edges AB, BD, CD and CA.
Prove that PQRS is a square.
What does this tell you about the opposite edges of the tetrahedron?
A triangle has sides 12, 13 and 15 units. Circles are drawn with centres at the vertices of the triangle so that each circle touches the other two.
Find the radii of the circles.
Can you always find touching circles for any triangle?
A photographer is taking photographs.
She has to arrange the people in two rows one behind the other in order of height.
Each person at the back must be taller than the person directly in front of them.
Along the rows the heights must increase from left to right.
How many different arrangements […]
2 x 3 x 4 x 5 + 1 = 11 x 11
21 x 22 x 23 x 24 + 1 = 505 x 505
Pick your own four consecutive numbers, find their product and add one. Is your answer a perfect square?
Show that if you add 1 to the […]
What is the sum of all the digits in all the integers from one to one million?
Don’t do a lot of tedious adding up – think mathematically!
Note: the digits in the integers from one to ten add up to 46
(not 55 because 10 contributes only 1 to this sum.)
The Olympic emblem consists of five overlapping rings containing nine regions.
Place the numbers 1, 2, 3, … 9 in the nine regions so that the total in each ring is the same.
Can you complete the solutions given in the 4 diagrams?
Choose four consecutive whole numbers, for example, 4, 5, 6 and 7.
Multiply the first and last numbers together (28).
Multiply the middle pair together (30).
Choose different sets of four consecutive whole numbers and do the same.
What do you notice about the difference between the two […]
Grade 4 ADDITION AND SUBTRACTION
Grade 5 MASS
Grade 6 ADDITION & SUBTRACTION 6 DIGIT NUMBERS
Grade 7 FUNCTIONS AND RELATIONS
Grade 8 FRACTIONS
Grade 9 ALGEBRAIC EXPRESSIONS
Grade 10 ANALYTIC GEOMETRY
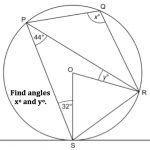
Grade 11 EUCLIDEAN GEOMETRY
Grade 12 EUCLIDEAN GEOMETRY
Click on a link above for […]
FOLLOW US ON SOCIAL MEDIA
