Triangular

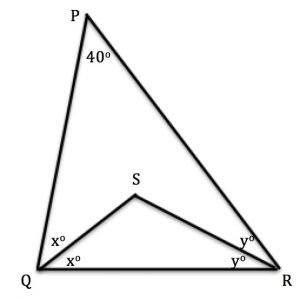Investigate different triangles PQR where the angle QPR is 40 degrees. Choose your own angles at Q and R, for example someone might choose 90 degrees and 50 degrees and someone else 62 degrees and 78 degrees.

Accurately draw the internal bisectors of the angles at Q and R to meet at S, as shown in the diagram.

What is the size of angle QSR?

Make you own conjecture about the size of angle QSR and prove it.

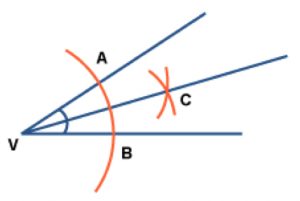This diagram shows how to bisect the angle at V.  You can either use a paperclip compass as shown in the video or ordinary compasses.

With centre V draw an arc of any radius and label the points A and B where the arc cuts the arms of the angle.

With centre A draw an arc. With centre B and the same radius draw an arc. These arcs cut at C. Join VC.

Then VC is the internal bisector of angle AVC, that is angles CVA and CVB are equal.

See the Notes for Teachers.