Posts by: toni
Investigating proofs of Pythagoras Theorem by similar triangles and practical jig-saw methods. Extension to the Cosine Rule.
Click here to download a pdf with all you need to run your own professional development workshop.
Introduction to the data handling cycle and collection and representation of data in a human pie chart and a variety of practical ways that involve the whole calss.
Click here to download a pdf with all you need to run your own professional development workshop.
People maths and paper folding and cutting to explore the concept of symmetry.
Click here for the Workshop Guide with all you need to run your own professional development workshop.
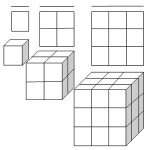
Investigations of angle properties of parallel lines, similarity in 2 and 3 dimensions and scale factors for linear, area and volume enlargement.
Click here to download a pdf with all you need to run your own professional development workshop.
These counting games lead to an understanding of multiples and common multiples, number patterns and the Sieve of Eratosthenes to find prime numbers.
Click here to download a pdf with all you need to run your own professional development workshop.
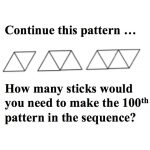
Copy this pattern. You could use toothpicks or paper sticks or draw the pattern on isometric paper (download here).
Make or draw the next 3 patterns in the sequence. How would you explain to someone else on the telephone how to do this when you could not point to the diagram?
[…]
JUST A MINUTE
How long is a minute? What can we do in a minute?
You will need: a stopwatch, paper & pencils (or other recording implements).
Activity 1: Estimate a minute
Sit with your head on your arms so that you will not be distracted. When the timekeeper says […]
If you are at row 0 column 1 (0 ; 1) how many columns do you go across and how many rows back would you go to get to row 2 column 4 (2 ; 4)?
Give directions for getting from row 1 column 0 (1 ; 0) to row 2 column […]
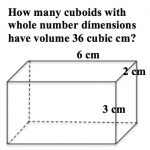
What is the volume of this cuboid?
How many other cuboids with whole number dimensions have the same volume?
Do any of them have the same surface area?
Which has the biggest surface area? Which has the smallest?
How many have a square cross section?
Click here for Notes for Teachers.
[…]
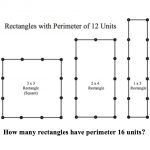
This activity is about rectangles with whole number dimensions. With other lengths and breadths there are infinitely many possible rectangles so here we just stick to whole numbers.
How many rectangles can you make with perimeter 12 units?
What do you know about rectangles? What is the smallest rectangle that you can […]
FOLLOW US ON SOCIAL MEDIA
