In how many ways can you fit all three pieces together, edge to edge, to make shapes with line symmetry?
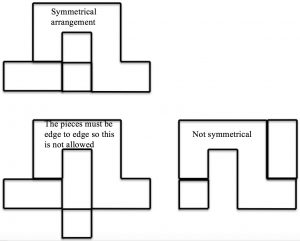The first of these examples shows a symmetrical arrangement, the second is not allowed because the pieces are not placed edge to edge and the third is not symmetrical.
Click here to download the REFLECTING SQUARELY worksheet from which you can cut out your own pieces and try different arrangements.
Click here to download the REFLECTING SQUARELY Notes for Teachers.
This problem is adapted from the NRICH task Reflecting Squarely with permission of the University of Cambridge. All rights reserved.
See nrich.maths.org/1840 for more about this problem.
If you enjoyed this article, please consider sharing it!
15 Responses to Reflecting Squarely
Leave a Reply
You must be logged in to post a comment.
FOLLOW US ON SOCIAL MEDIA
You can fit these thins in five ways
I think you can fit these pieces in six ways
The final answer is not important (and is not any of the above!). What is important is how you can use this problem with your learners to explore symmetry? If you have tried this with your learners how did they do? Is there anything you could do to support struggling learners? Is there anything you could do to help push the more confident learners?
Sometimes learners become confused about understanding symmetry but the bottom line is that an object has to be cut into two halves regardless on how it done for an example if you if you allow learners to do a graph of a parabola for them to be accurate in getting the symmetry they should plot the graph and fold it in the middle so that each side overlap on top of each other.
In preparing the lesson we will cut out the shapes for the learners.
Arrange the class in groups of 3/4. We will explain how the blocks can be attached to each other.
Ask the learners the prior knowledge about the line of symmetry.
We make the concept of line of symmetry clear to the learners.
Ask each group to put their shapes using the pieces, and draw them on their exercise books and find the line of symmetry the shape.
This will be done in class.
In a class of 58 I would group my Learners into smaller groups of 6.
First of all, I would make them understand the meaning of the term symmetry.The first demonstration would be done by me so that they see that what I want them to do is possible and show them what I mean by the line of symmetry.
I would bring to their attention that there are numerous possibilities that can come out of different arrangements with similar results.
Then I would let them loose to explore their own shapes, encouraging those who have come up with a particular shape to post it on the wall with the group’s names.
The class should clap hands for those who have come up with a different shape.
reflection or symmetric:
First you need to explain to the learners what how symmetrical means.Example will be the slice of bread when you want to make a sandwitch.When you cut the slice of bread in to two equal halves.weather you cut it through the middle or from one corner to the other. the part that you cut is a line of symmetry, because you have identical two parts(Half slice).
Then you place the squares, showing them which way will not be exceptable.like when the one of loose piece overlap and when the line of symmetry does not cut into to identical pieces.
I’l have to give them certain type of shape(might be a triangle or a square ) so as to make them understand the line of symmetry after all i’l give them more shapes(hexagons,octagons,etc) to play them around looking for lines of symmetry and i can use some art sculptures to continue doing the same and then in the course of the week when I’m sure they know the meaning of line of symmetry i’l give them these above 3 shapes to play with and try to find as many different shapes that possesses line of symmetry.
we have to ask for their prior knowledge of the lines of symmetry. after we have discussed their understanding,we explain the line of symmetry. we have to discuss *why the line of symmetry in any drawing*.We will talk of square, the symmetry line will divide our square into two equal parts.after that I will give more examples of triangles with lines of symmetry.Then i will give these pieces to form shapes with lines of symmetry, they will form many as possible.
Teacher provide of all the necessitous to learners,like scissors, copies of the figure needed to be cut out. Id mention the possible amount of solution they should be getting(just to give them an idea what to work with). Demonstration is essential in this regard and learners have to discover the rest themselves. Make MUST make make use of optimum and maximum time in class to prevent plagiary. Draft a rubric to assess, reasoning that rubric provide reflexibility cause there can be no wrong answer!
Firstly I have to group my learners into groups. I have to ask them prior knwoladge (what does they know about symetry)after that I’ll give them a paper to cut those shapes. Each group must come up with different shape and each groupmut make sure that when he/ she drawn the lines of symetry left hand side must same with right hand side. Then when you finished,one learner in your group must come into the board to draw and show us line of symetry.
What I can do when teaching my learners this topic, I’ll group them into groups of 4 (in my large class of 103 they can be 6). Try to check the experince that they have about the line (s) of symmetry. Then, give them pieces in the form of worksheet. And each group try to find out all the possible moves that they can take to fit these piece, and finally one person from each group must go to the board to draw what they have discovered in their respective groups and also draw the line of symmetry. Learners need to know the meaning of the line of symmetry, so it can be much more helpful to give them the picture of deviding something into to two symmetrical parts.
And also, I can give learners from other group an opportunity to check whether what is written on the board is correct or not.
For the planning of the lesson you always move from known to unknown. Firstly i would want to know from them if they have any knowledge of the line of symmetry. If so I would then give them different shapes and ask them to identify how many lines of symmetry can be found.Then when i am satisfied that they have done a good job i would group them into groups of 5, give them the shape to cut out and ask them to join them and identify all the lines of symmetry of rotation. i would then make a rubric to assess their work
Learners would be given this activity to reinforce reflection and symmetry.
Carefully explain to learners what the task entails and remind them that all pieces can be moved around.
It might also be useful to remind them of lines of symmetry in different levels ( horizontally, diagonally,etc…)
The activity would be given to individual learners in small classes, but to small groups in bigger classes.
Learners would be required to start the activity in class and encouraged to find as many different arrangements as possible.
All will be allowed to work on it for 5 minutes after which those who have completed any will be asked to share solutions with others on the chalkboard.
In bigger groups each learner in the group will be asked to come up with a different reflection to ensure that all are engaged.
As new shapes come up, it is written on the chalkboard.
Only tell them at the end of the period how many possibilities there are and task them to find solutions as homework for the following day.
I am going to show an example of symmetry by letting learners to open their palms of their hands and indicate to them when hands are put together on edges that the left hand is symmetrical to right hand and he line on the edges is called a line of symmetry.Secondly let them draw a square and let them cut into two halves and ask them what do we call the line which divides the square into two halves ,taking from the example of the palms.Thirdly ;take the square paper and flip it and let them identify the line of symmetry.Give them the paper with these three pieces and let them cut and organize different shapes when fitting the piece to show symmetry. They must give as many as they can.