Archimedes (287 BC – 212 BC) wrote about problems like this involving touching circles.
The outer circle, centre O, has radius 2 units.
The points O, A, A’, B and C are centres of circles that are tangent to each other where they touch.
It can be shown that OACB is a rectangle.
- Prove that OA is perpendicular to OB.
- Find the radii b and c and the ratio of the radii of the circles with centres A, B and C.
What do you notice about triangle OAB?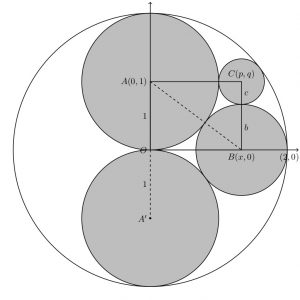
The second part of this activity is a challenge for students who are not daunted by having to do a lot of algebra:
The proof that OACB is a rectangle can also be done using coordinate geometry, the formula for the distance between two points and the fact that the circles all touch each other.
1.Use Pythagoras Theorem for \triangle AOB and the fact that the circle centre B touches the outer circle to show that b = \frac{2}{3} and x = \frac{4}{3}.
2. The circle centre C touches 3 other circles, using this:
a) Write down 3 equations involving p, q and c and, from them, 3 expressions equal to p^2 + q^2 -c^2.
b) Find 3 linear expressions involving p, q and c.
c) Find an expression giving p in terms of c.
d) Find an expression giving q in terms of c.
e) Eliminate p and q to produce a quadratic equation in c and solve this equation to find c.
3. For each value of c, find p and q and identify the two circles to which these values correspond.
4. Explain why the values found show that OACB is a rectangle.
Click here to download the KISSING CIRCLES worksheet.
Click here for the Home Learning Guide.
Click here for the Notes for Teachers.
If you enjoyed this article, please consider sharing it!
FOLLOW US ON SOCIAL MEDIA
