Tessellating Quadrilaterals
We say that a shape tessellates if we can fit together copies of it to cover a flat surface without leaving any gaps and this covering can be extended in all directions.
The question here is “What can we find out about tessellating different quadrilaterals?”
It’s quite easy to see how squares tessellate.
What about other types of quadrilateral?
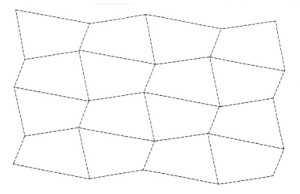
Have a go at drawing some quadrilaterals, and finding ways to make them tessellate. You might like to cut a quadrilateral from scrap cardboard and use it to draw around again and again to make a tessellation.
Think about different types of quadrilateral. For example, can you find a way to tessellate any parallelogram? What about a kite? Or a trapezium?
What do you notice about your tessellations?
Do all quadrilaterals tessellate? If your answer is no, give an example of a quadrilateral which doesn’t tessellate. Can you explain why it doesn’t tessellate?
If your answer is yes, can you explain why all quadrilaterals tessellate, and can you give a method which will produce a tessellation of any quadrilateral?
Click here to download Notes for Teachers.
This problem is adapted from the NRICH problem with the same name with permission of the University of Cambridge. All rights reserved.
South Africa COVID-19 News
Here is the official website for COVID-19 updates.
Login
SUPPORT AIMSSEC





