Currently viewing the tag: "Number patterns"
1.1 The square grids below the continuous line depict negative numbers and those above the line positive numbers. Study the square grids shown above with black squares forming a pattern. How is the pattern growing? Create square grids 9, 10 and 11; complete them with black squares to further develop the […]
Start by watching the video https://youtu.be/B2dkNPaTmDY
Each student should have a stage 3 Sierpinski triangle of edge length about 6.5 cm and a colouring pen, and should colour their triangle as shown by the black filling in the small diagram.
The class will make poster of a stage […]
1. If the red square has area 1 square unit. What is the area enclosed by the stage 1 squareflake?
2. What is the area enclosed by the stage 2 squareflake? What about the stages 3 and 4 squareflakes?
3. If replacing each line segment on the edge with the zig-zag is […]
The curve, also known as the ‘snowflake curve’, was invented in 1904 by the Swedish mathematician Helge von Koch.
Take a large piece of backing paper, and either draw an equilateral triangle with edges of length 27 cm or cut a triangle from coloured paper and stick it on […]
Can you see what the rule is for filling numbers in the hexagons? Continue the pattern using the same rule. If you get it right the bottom row will start 1, 9, 36, 84, …
Shade the hexagons where the number inside is odd all in one colour. Using a contrasting colour, […]
What patterns do you notice in this table?
Continue the patterns to fill the empty squares.
Write a list describing all the patterns that you see.
What do you notice about the numbers on squares of the same colour?
Would the patterns […]
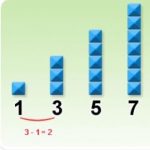
How to use beans, stones and other objects to form pattern sequences and to develop an understanding of algebraic formulas.
Click here to download a PDF with all you need to run your own professional development workshop.
Work out the different numbers to replace the question marks.
What do you notice about the patterns in these calculations?
Can you explain why this pattern occurs?
Describe and explain this pattern.
What do you think the patterns for other multiples look like, for example multiples of 2 or 3 or 4 or 5?
Download this sheet and shade in the patterns of the multiples.
Why do you think that in each pattern […]
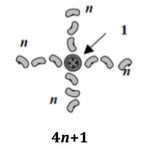
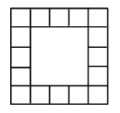
This square of squares pattern has edge length 5 squares. You could make this pattern with 48 matchsticks.
Work out the number of edge squares and the number of lines (matchsticks) needed to make the pattern with: side length 6, side length 25, side length 100, side length n.
Click here […]
FOLLOW US ON SOCIAL MEDIA
