Currently viewing the tag: "Number patterns"
What patterns do you see in them?
Suppose you have to share 9872 gold coins between 8 people.
You give the coins out in thousands until there are less than 8000 left.
Then you give out one hundred at a time until there are less than 800, then […]
Ram had 15 coins, all the same kind, and he put them into 4 bags.
He labelled each bag with the number of coins inside it.
He could then pay any sum of money from 1 coin to 15 coins using one or more of the bags without opening any of the bags.
How […]
1. What do you see in this picture?
Give a proof linked to this picture of the formula $a^2 – b^2 = (a + b)(a – b)$ .
2. What do you notice about the difference between squares of consecutive numbers?
Compare the differences between squares of numbers that differ by 1 […]
Is a picture worth a thousand words, as the saying goes?
This picture shows the first 4 triangle numbers: 1, 3, 6 and 10 and how you can fit 2 identical copies of a triangle together to form a rectangle.
Can you use it to find the number of dots in the […]
First complete the number sentences by putting = + – x or ÷ in the boxes. Then explain why the pattern occurs.
Explore the pattern you get when you carry on these multiplications up to 37 × 54.
Click here for MAGIC OF 37 worksheet.
Click here for the Notes […]
You might like to start by investigating the patterns you get when you shade multiples of a number on a grid. Download here
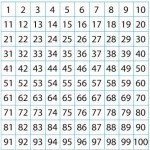
For the prime sieve investigation use a 100 square grid (download here):
Circle the number 2. Put a line through every multiple of 2 up to 100.
[…]
Can you find the chosen number from this square using the clues below?
1. The number is odd.
2. It is a multiple of three.
3. It is smaller than 7 x 4.
4. It has an even tens digit.
5. It is the greater of the two possibilities.
[…]
Fibonacci (in the year 1202) investigated a problem about how fast a population of rabbits would grow in the following circumstances, starting with just one pair of rabbits:
Suppose a newly-born pair of rabbits, one male, one female, are put in a field. Rabbits are able to mate at the age of […]
In sheep talk the only letters used are B and A.
Sequences of words are formed as follows:
The first word only contains the single letter A.
To get the next word in the sequence change each A in the previous word into B and each B in the previous word […]
Complete the calculations in the picture.
What do you notice?
To explain how the patterns of numbers arise:
Either multiply by (10 – 1) instead of multiplying by 9
or use the table below, first completing the calculations on each line.
FOLLOW US ON SOCIAL MEDIA
