Currently viewing the tag: "Angles"
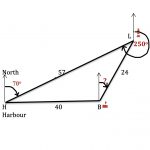
(1) A small boat leaves a harbour H and travels due East (bearing 090 degrees) for 40 km to a marker buoy B and then sails directly towards a lighthouse L which is 24 km from B. It then returns to the harbour H, that is a distance of 57 km on […]
Why does this fold create an angle of sixty degrees?
Make a centre crease down the length of the paper then open it up.
Next fold one corner over and onto the centre crease so that the fold line passes through the corner next to it (on the short side of the paper).
You […]
Take any triangle and label it ABC with A as the largest angle. Fold the triangle along PQ, PS and QT where the points P and Q are the midpoints of AB and AC and PS and PT are perpendicular to BC.
What do you notice? Why does this happen? Will it […]
What do you know about robots? What are drones? Are driver-less cars actually robots? What do you think about robots that move around warehouses to pick up and carry loads from place to place or control complicated machinery in factories? What do you think about robots that mow lawns and clean floors?
[…]
A square of paper 8 cm by 8 cm is folded so that the corner P coincides with the midpoint of an opposite edge as shown in the diagram.
Investigate the three triangles (where there is a single thickness of the paper) that are formed by folding in this way.
Click here for […]
For any triangle you can construct a line through one of the vertices parallel to the opposite edge.
Using what you know about angles and parallel lines prove that the angles of the triangle add up to 180 degrees.
Click here to download the ANGLE SUM worksheet.
Click here […]
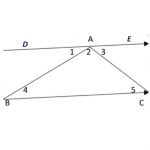
This diagram shows 3 sets of parallel lines. What do you notice in the diagram?
Look at the triangle with angles marked 1, 2 and 3.
Call this T.
Label angles equal to these angles. Why are they equal?
Look at the larger heavily outlined triangle.
How many copies of triangle T can […]
The picture shows you how to use a paper clip to draw circles. You just need to open out the paper clip as shown,
Draw a circle and mark 24 points equally spaced around the circumference. To do this, draw a circle and mark the centre, and mark your first point on […]
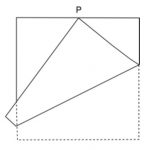
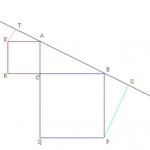
In the diagram ASRC and BCQP are squares and PU and ST are perpendicular to the straight line TABU.
Prove that PU + ST = AB.
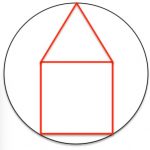
This shape is an equilateral triangle sitting on top of a square.
What is the radius of the circle that circumscribes the shape?
Click here for a hint if you need one to get started.
Click here for the Notes for Teachers.
Click here for the ENCIRCLING poster.
[…]
FOLLOW US ON SOCIAL MEDIA
