Same Birthday
 In a group of 23 people there is more than a 50% chance that two will have the same birthday? Does that surprise you?
In a group of 23 people there is more than a 50% chance that two will have the same birthday? Does that surprise you?
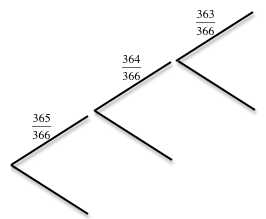
Including February 29th how many different birthdays can there be? Start with any 3 people A, B and C. What is the probability that B has a different birthday from A? What is the probability that A and B have different birthdays and C has a different birthday from A and from B?
For a group of 3 people what is the probability that two will have the same birthday?
What about a group of 4 people? Or a bigger group?
Can you do the calculations to work out the probabilities?
Click here to download the SAME BIRTHDAY worksheet.
Click here to download the Notes for Teachers
10 Responses to Same Birthday
Leave a Reply Cancel reply
You must be logged in to post a comment.
South Africa COVID-19 News
Here is the official website for COVID-19 updates.
Login
SUPPORT AIMSSEC






At the workshop on 18 February, of the 57 teachers who recorded their birthdays, there were 7 pairs who shared the same birthday.
Chris told one class he taught that he would give them a day free from homework if they all wrote down a number between 1 and 100 and no two learners in the class had the same number. They thought they would be lucky and get no homework but Chris knew better!
Their homework was to work out the probability of two of them having written down the same number. This is just another variation on the birthday problem. With 30 learners in the class this probability is 0.992 (to 3 decimal places) so there was a very small chance that they would have escaped the homework.
I suggest you try this with your learners and let us know what happens.
Now you can download and study the notes for teachers and solutions. Later in the year when you have done more work yourself on probability, and when you are teaching it for your learners, we suggest you give your learners this problem to do, but first build up to it with the Same Sweets problem (n=5), the children in families (n=2) and the Same Birth-month problem (n=12).
It may seem a hard problem but we need to have high expectations for our learners in South Africa. If you ask too little of learners they will not achieve to their full potential. They are just as clever as learners anywhere in the world but they are doing very badly and teachers must work to change that.
I am still confused with this sharing of birthdays because ,I want to work out the probability of sharing ,not the probability of not sharing. Could you please explain to me why do decided to give an example of probability of not sharing.Is the probabilty of not sharing birthdays and of sharing birthdays complementary to each other?
You are right. These are COMPLEMENTARY events. The probabilities of an event happening and not happening are complementary and add up to 1.
This time it is easier to work out the probability of not sharing and subtract it from 1.
No what you say is not correct. You need to think again. Read the solution in the Notes for Teachers which you can download above and if you don’t understand the solution then you can ask about it again.
To start to put right what you have written above, though it does not help solve the Birthday Problem, if you choose 3 people, then the probability all 3 people having the same birthday is (1/366)x(1/366) which works out at about 7 in a million. The reason is that the probability of the second one having the same birthday as the first is 1/366 and the probability of the third one having the same birthday is again 1/366 so you multiply these probabilities to get the answer. Does that make sense to you?
Thank you,now I can understand I was wondering why do you have to multiply these probabilities.Does that mean the probability the probability of 15 would be 1/366 fifteen times?
Think of a simple example: Suppose the probability that event A happens is 1/3 and the probability that event B happens is 1/2. This means that event B only happens (on average) on half the times event A happens. So the probability of both happening is 1/6. We multiply 1/2 by 1/3 to get 1/6.
This is the reason behind multiplying the probabilities on the branches of a tree diagram.
If you have a group of 15 people the probability of them ALL having the same birthday is (1/366) raised to the power 15.
But this problem is not asking that they ALL have the same birthday. It asks “what is the probability that a pair of people from the group have the same birthday?”
The birthday problems will help our learners to think independently. During the assigned period in the workschedule for teaching Probability I will use those. What I understand is that sharing and not sharing are complementary. I will build learners thinking on such.
The birthday problems are good challenging scenarios. When the time comes I will give such problems to learners. I will build their understanding on the idea that sharing and not sharing birthdays are complementary.
Think carefully! The number of possible birthdays is 366 (number of days in a leap year) not 7 or any other number. Think what you do with the probabilities in a tree diagram – you multiply probabilities for successive events.
Read the question. Work out the probability of everyone in a group having DIFFERENT birthdays (starting with a group of 2 people and then 3, then 4 and so on). Subtract this from 1 to get the probability that at lease two people have the same birthday because these are COMPLEMENTARY events.
Don’t give answers here. This is the place for discussion of how to use these problems in lessons.