The probability that there are two people in a group with birthdays in the same month depends on the size of the group.
What if the group has more than twelve people?
What about a group of 2 people? What is the probability they have birthdays in different months?
What about a group of 3 people? Let’s call them A, B and C. Suppose A and B have birthdays in different months. What is the probability that C’s birthday is in a different month from A and B?
What is the probability that A, B and C all have birthdays in different months?
What is the probability that two of them have birthdays in the same month?
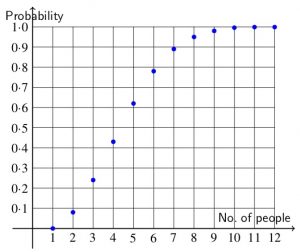
For larger groups, calculate the probability f of two people in the group having birthdays in the same month. The table and graph below give you some of these answers.
A tree diagram is useful, but you don’t need to draw all the branches.
The challenge is to understand and to be able to explain the method.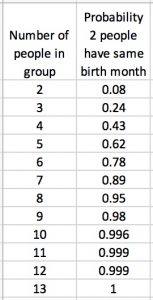
Click here to download the SAME BIRTHDAY worksheet
Click here to download the SAME BIRTHDAY Notes for Teachers
If you enjoyed this article, please consider sharing it!
8 Responses to Same Birth-month
Leave a Reply
You must be logged in to post a comment.
FOLLOW US ON SOCIAL MEDIA
the probability that the two will have same month is 11 out of 12,
the probability that the third one will share a birtday with one of the two is 10 out of 12
Can you see why you must MULTIPLY 11/12 by 10/12 to get the probability that no two people in a group of 3 have the same birth-month?
You might like to introduce your learners to this problem and share your experiences with other teachers on this forum.
Yes Toni I think I understand this one But will introduce it on the 4th quarter toni as per our guide from the department of education.
There is one that I dont understand, the one about birthdays. why does that graph on DHP(probability says a group of 60 people has 100% chance of having two people sharing the same birthday?
Good question Nelly. It is not exactly 100%, it is actually 99.4%. The probability that there are two people in a group with the same birthday is not EXACTLY 100% until you have a group of 366 people.
For 60 people it is worked out as
[1 – (365 x 364 x 363 x 362 x … x 307)/366^59]
where 366^59 means 366 raised to the power 59.
if they are more than 12 the probability is 1
1. 2people will share same month.
2. 2/12
3. 1/12
4. 3/12
5. 2/12
Zuzaz, I can’t understand what your numbers mean. Anyway you have a link above by which you can download the solutions and the notes for teachers. These comment boxes are not for giving answers – there is no purpose in that. There might be some purpose in discussing the explanations but your message includes no explanations.
The main purpose of these comment boxes is for discussion of how to use these problems to help our learners to think mathematically and to become better problem solvers themselves.
I really enjoyed the DHP activity on the same birthmonth. I cannot wait to teach it to my Grade 10 learners. They don’t particulartly enjoy probability, but if we could make it more practical and have them included in the lesson, instead of just working with situations from the textbook, I bet they would have more fun. I feel if learners enjoy the way they learn new aspects, they remember it longer.
Good night, ALL.