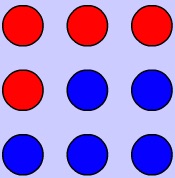(a) You must mark four red squares and five blue squares in a 3 by 3 grid .
How many ways can you do this so that all the rows columns and diagonals have an even number of red squares?
Two solutions are considered the same if one can be transformed to the other by rotating the square.
(b) Are there any additional solutions if only the rows and columns need to have an even number of red squares?
Click here to download the RED EVEN worksheet.
If you enjoyed this article, please consider sharing it!
FOLLOW US ON SOCIAL MEDIA
