Pythagorean Triples and Incircles

Investigate inscribed circles of right-angled triangles that have edges of integer length.

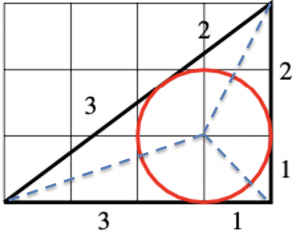(1) Draw a 3-4-5 right-angled triangle on a grid. 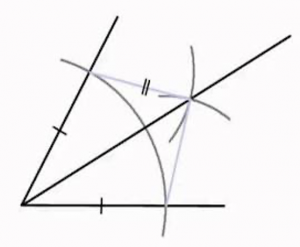Using compasses construct the internal bisectors of the angles of the triangle and then draw the inscribed circle (we’ll call it an incircle). What do you notice?

(2) Repeat this for a 5-12-13 right-angled triangle and then for an 8-15-17 right-angled 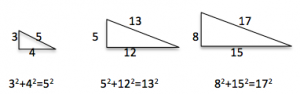triangle. Does the radius of the incircle have integer length for the triangles given by the three Pythagorean triples 3-4-5, 5-12-13 and 8-15-17?

(3) To prove the general result that the radius of the incircle is an integer for all right-angled triangles with edges of integer length you will need to use algebra and the formulae for generating Pythagorean Triples.

The formula is: for any two whole numbers p and q then the triangle with integer edge lengths  $p^2 + q^2, p^2 – q^2$ and 2pq is right angled. Check this using Pythagoras Theorem.

(4) Check that, p = 2 and q = 1 gives the 3–4–5 triangle,

p = 3 and q = 2 gives the 5–12–13 triangle and,

p = 4 and q = 1 gives the 8–10–17 triangle.

What triple do you get by taking p = 4 and q = 3?

See Wikipedia for more information. This is a list (in a different notation) of all the Pythagorean Triples for triangles with edge lengths less than 100, not listing enlargements of these triangles.

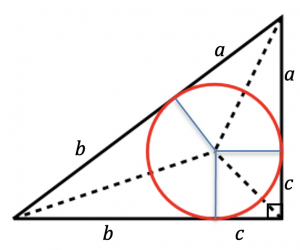(5) Theorem For all right-angled triangles with integer edge lengths, the radius of the incircle is an integer. To prove this Theorem:

(i)Write down three simultaneous equations giving a + b, b + c and c + a in terms of p, q and r.

(ii) Solve the equations to give a, b and c in terms of p, q and r.

(iii) Prove that the radius of the incircle is equal to c and c = q(p – q) which is an integer.

Click here to download a worksheet for Pythagorean Triples and Incircles.

Click here to download the notes for Teachers for Pythagorean Triples and Incircles.

Click here to download a poster for Pythagorean Triples and Incircles.

Click here to download a pdf that provides both a framework and activities for

workshops for teachers and teaching resources for learners on Pythagoras Theorem and its generalisation to the Cosine Rule.