Which of the following products are close to 1368:
20 x 40 20 x 50 20 x 70
40 x 50 40 x 70 or 50 x 70?
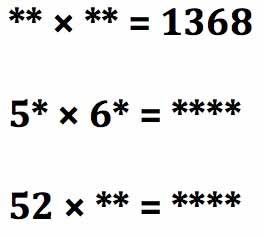In these three multiplication sums, using the digits 1 to 8 once and only once each time, can you replace the * symbols and make the multiplications correct?
Can you explain how you found the answers?
See Notes for Teachers – One to Eight and the NRICH website for further information and learners’ solutions.
If you enjoyed this article, please consider sharing it!
4 Responses to One to Eight
Leave a Reply
You must be logged in to post a comment.
FOLLOW US ON SOCIAL MEDIA
should i have the sama answer on all the 3 sums?
These are three DIFFERENT multiplication sums with three different answers.
In each one the digits 1, 2, 3, 4, 5, 6, 7, & 8 appear once and only once.
Working systematically you will find that there are only 2 possible cases to test out in the first problem and only 10 possible cases in the second and again 10 cases in the third problem. With a calculator you can very quickly check 10 cases.
These discussion boxes are for teachers to share ideas about how they used the problems to help learners to develop problem solving skills.
What ‘Key Questions’ did you ask in your lesson?
i manage to do the first two.
24 x 57 = 1368…… i tried from 21 up to 24 then i got the answer. it was trial and error
the second one is 58 x 64 = 3712. again this was trial and improvement.
I can not link this to any lesson for my class, please help me.
See page 36 of the CAPS document where it refers to teaching Multiples and Factors at Grade 7 and also to problem solving. It says:
“Revise the following done in grade 6:
-Multiples of 2 digit and 3 digit whole numbers
-Factors of 2 digit and 3 digit whole numbers
-Prime factors of numbers to at least 100.”
and also:
“* Practice with finding multiples and factors of whole numbers is especially important when learners do calculations with fractions. They use this knowledge to find the LCM and also when they simplify fractions and have to find equivalent fractions.
* Factorising whole numbers lays the foundation for factorisation of algebraic expressions.
*Using the definition of prime numbers emphasises that 1 is not classified as a prime number.”