Do this as you read…
Think of a number.
Multiply it by 3.
Add 6.
Take away your number.
Divide by 2.
Take away your number.
You have finished with 3.
How does this work?
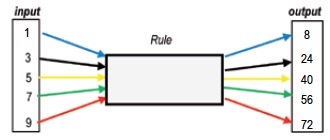The Function Game is an extension of this Mind Reader activity. What is the rule (or function) that gives the outputs corresponding to the inputs shown in the diagram mapping 1 to 8 and 3 to 24 etc?
To play the Function Game, the teacher thinks of a function, the learners suggest numbers (inputs) and the teacher, telling them that she is doing the same operations each time to their number, writes the outputs on the board. The learners have to guess what rule the teacher is using (what function). When a learner thinks she has guessed the rule the teacher gives her an input and if the learner gives the corresponding output the teacher tells her she is correct. The game continues until several of the learners have guessed the rule and then one of the learners explains to the class how she found it. For example if the function is x \to 3x+5 then 2 \to 11, 3 \to 14, 10 \to 35 etc.
Click here to download the MIND READER worksheet.
Click here for Notes for Teachers.
This problem is adapted from the NRICH task with the same name with permission of the University of Cambridge. All rights reserved.
If you enjoyed this article, please consider sharing it!
4 Responses to Mind Reader
Leave a Reply
You must be logged in to post a comment.
FOLLOW US ON SOCIAL MEDIA
Remember this conversation should be about how you use the problems in teaching. Don’t just give answers. This is not about answers it is about teaching. Let’s have a professional discussion where we give reasons and not just give opinions.
Why do you think that it is a challenging problem for grade 9?
What will the learners gain if the teacher avoids explaining why everyone gets the answer 3 whatever number they start with?
What will the learners lose if the teacher gives the explanation?
How will you encourage the learners to explain why it happens?
Did your learners think of using algebra or did you suggest that they use algebra.
Did your learners discuss it in pairs or in groups?
Did some of the learners find the explanation for themselves?
Did you perhaps give learners the homework task of solving the ‘mystery’ so that they would have more time to find a solution?
How does it feel as a teacher to hold back and not to give an explanation so that learners enjoy the experience of thinking for themselves? Were you tempted to tell them? If so, how did you manage to restrain yourself?
So we want the learners to use algebra but we don’t want to tell them to use algebra. It is difficult being a teacher who wants to encourage their learners to think! Practical apparatus can help. You will need 3 small boxes that look the same and some counters or stones or ask the learners to bring boxes and counters.
Think of your number and put that number of counters into each of the boxes.
Think of a number
Take one box inside is your secret number of counters
Multiply it by 3
So set out three boxes, shake to show they each have counters inside
Add 6
Next to your three boxes set out 6 extra counters
Take away your number
So take away one box
Divide by 2?
Take away your number?
Can your learners see how to carry on and divide by 2.
If you are lucky they will all end up with just three counters.
They can then repeat writing x for the box and make a list like this. ( I haven’t used equals signs because you can easily write down complicated expressions which aren’t true. All we need is a list showing the algebraic expression at each stage)
Think of a number x
Multiply it by 3 3x
Add 6 3x + 6
Take away your number 2x + 6
Divide by 2
Take away your number
Does anyone know another problem like this which learners might like to try next?
Christine
I used it as an introduction to algebra in Grade 9, most learners managed to get the correct answer and one was able to explain why the answer is 3. From there we substituted the number with x and they got the same answer and my lesson was successful.
It was so nice as I act as if if I had Magic powers, every one wanted to prove that I dont have MAGIC.
As time goes by i took off the part which say subtract at the end and ask them to show me the answers so that I use my magic power to tell them the number they first thought.
As I was busy pouring the quiz questions their interest to prove that i dont have magic improved. At last they saw that i m doing inverses and they see the reason of their answers to be the same while they didnt think one number.