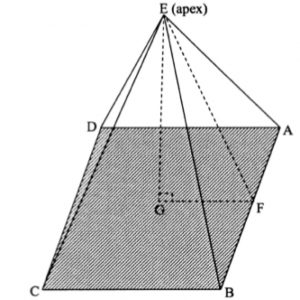
The Great Pyramid at Giza in Egypt was built around 2500 BC. The pyramid has a square base ABCD with sides 232.6 metres long. The distance from each corner of the base to the apex E was originally 221.2 metres.
You may find it helpful to make a square based pyramid with paper sticks and cut out a paper triangle like triangle EGF to fit inside.
Draw a diagram of the pyramid to show two right angled triangles from which you can write down trigonometric equations to answer the following questions.
- If F is a point on AB such that EF is perpendicular to AB and G is vertically below the apex E , what can you say about triangles EFA and EGF?
- Calculate the size of the angle at the apex of a face of the pyramid (for example angle AEB). Can you find this by two different methods?
- Calculate the angle each face makes with the base (for example angle EFG)
Click here for the GREAT PYRAMID worksheet.
If you enjoyed this article, please consider sharing it!
FOLLOW US ON SOCIAL MEDIA
