Great Pyramid
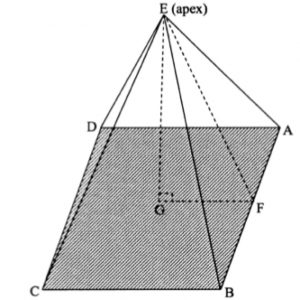
 The Great Pyramid at Giza in Egypt was built around 2500 BC. The pyramid has a square base ABCD with sides 232.6 metres long. The distance from each corner of the base to the apex E was originally 221.2 metres.
The Great Pyramid at Giza in Egypt was built around 2500 BC. The pyramid has a square base ABCD with sides 232.6 metres long. The distance from each corner of the base to the apex E was originally 221.2 metres.
 You may find it helpful to make a square based pyramid with paper sticks and cut out a paper triangle like triangle EGF to fit inside.
You may find it helpful to make a square based pyramid with paper sticks and cut out a paper triangle like triangle EGF to fit inside.
Draw a diagram of the pyramid to show two right angled triangles from which you can write down trigonometric equations to answer the following questions.
- If F is a point on AB such that EF is perpendicular to AB and G is vertically below the apex E , what can you say about triangles EFA and EGF?
- Calculate the size of the angle at the apex of a face of the pyramid (for example angle AEB). Can you find this by two different methods?
- Calculate the angle each face makes with the base (for example angle EFG)
Click here for the GREAT PYRAMID worksheet.
South Africa COVID-19 News
Here is the official website for COVID-19 updates.
Login
SUPPORT AIMSSEC