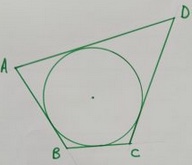Investigate quadrilaterals that have inscribed circles as shown in the diagram.
Draw a circle with any radius you choose, and then draw 4 tangents making a quadrilateral with the circle inside touching the quadrilateral at 4 points.
Measure the edge lengths of the quadrilateral ABCD.
What do you notice?
Copy the table below with 8 columns and write the details of your own special quad in the first row. You could try this with different quadrilaterals that touch the same circle or with different circles.
What do you notice? Write down your own conjecture.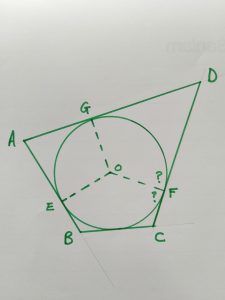
Can you prove your conjecture?
Draw the radii to the points of contact E, F, G & H, and measure the angles between the radii and the tangents.
What do you notice?
Now draw line segment AO. Can you prove that Δ AEO ≡ Δ AGO?
Compare lengths AG and AE. What does this suggest about AB + CD and about BC + DA?
Click here for Notes for Teachers.
If you enjoyed this article, please consider sharing it!
FOLLOW US ON SOCIAL MEDIA
