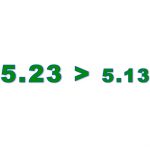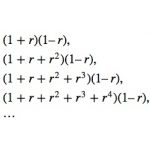Class 4 have made a bar chart showing the months of their birthdays.
Which is the month with no birthdays?
Which months have four birthdays?
How many children are in the class?
Make a birthday bar chart for your class by writing your name or initials in one […]
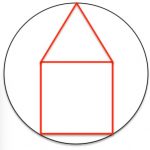
This shape is an equilateral triangle sitting on top of a square.
What is the radius of the circle that circumscribes the shape?
Click here for a hint if you need one to get started.
Click here for the Notes for Teachers.
Click here for the ENCIRCLING poster.
[…]
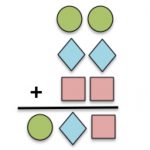
The challenge is to find numbers to replace the shapes and to make this addition sum correct.
Hint: Imagine adding up the tens column.
What number do you think has to go in the hundreds place? Why?
In the simpler number puzzles 1. and 2. put different numbers in place of the […]
Your Granny bought a bar of chocolate marked into 32 pieces and weighing 180 grams.
How many pieces make half the chocolate bar?
How many pieces make one quarter?
What fraction of the bar is one piece of chocolate?
She gave you and your sister 2 pieces each to eat. What fraction […]
These images are not shown to the same scale. An elephant is much bigger and heavier than a cat or a car. Can you arrange these things in order from lightest to heaviest? Can you estimate the mass of each of these things?
Use the symbols > < 1 1 2 3 in the boxes to make correct number sentences.
For example 5.12 < 5.13 is correct and 5.21 >5.23 is wrong.
How many different sentences can you make?
How will you know when you have found them all?
Click here […]
Imagine you have four bags containing a large number of 1s, 4s, 7s and 10s.
You can choose numbers from the bags and add them to make different totals. You don’t have to use numbers from every bag, and there will always be as many of each number as you need.
Choose some […]
Multiply out these expressions:
What do you notice?
Does this pattern continue?
Can you prove it?
What does this tell you about the sum to n terms of the geometric series with first term 1 and common ratio r?
Why do we get a formula for all values of r except r = 1?
Explain […]
Angles A, B and C are the angles of a triangle. Decide whether each of the following is an identity, always true for all triangles, or an equation, sometimes true. If you decide it is an equation find the solution or solutions and describe the corresponding triangle.
The angle of elevation from a point C on the ground, at the centre of the goalpost is 64.75 degrees to the highest point A of the arc, directly above the centre of the Moses Madhiba Soccer Stadium in Durban. The soccer pitch is 100 metres long (PQ in the diagram) and […]
South Africa COVID-19 News
Here is the official website for COVID-19 updates.
Login
SUPPORT AIMSSEC