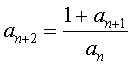Posts by: toni
Here you see the front and back views of a dodecahedron which is a solid with pentagonal faces.
Using twenty of the numbers from 1 to 25, each vertex can be numbered so that the numbers around each pentagonal face add up to 65.
The number F is the number of faces […]
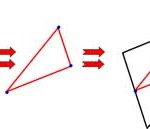
You are only given the three midpoints of the sides of a triangle.
How can you construct the original triangle?
Is there more than one way to find the answer?
What similarities and differences can you see between this Triangle Midpoints problem, The Checkit Game with Addition https://aiminghigh.aimssec.ac.za/checkit-game/ and Polycircles https://aiminghigh.aimssec.ac.za/polycircles/
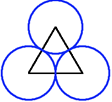
If you take the edge length of the equilateral triangles in this picture as the unit for length, what would be the exact size of the hole ?
Alternatively, if the area of an equilateral triangles is taken as the unit for area, what size is the hole?
Click here for Notes for […]
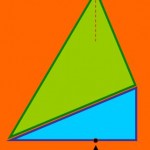
Two right-angled triangles are joined as shown in the diagram.
The green triangle has side lengths of 65, 52 and 39 cm and the blue triangle has side lengths of 52, 48 and 20 cm.
An object is dropped vertically from the top of the green triangle hitting the base by […]
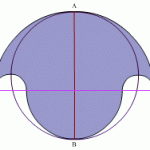
This shape, which is constructed using four semi-circles, is called a Salinon.
If the radius of the larger blue semicircle is a and the radius of the smaller blue semicircle is b, what are the radii of the smallest semicircles?
What is the relationship between the area of the shaded region and the area […]
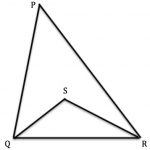
Investigate different triangles PQR where the angle QPR is 40 degrees. Choose your own angles at Q and R, for example someone might choose 90 degrees and 50 degrees and someone else 62 degrees and 78 degrees.
Accurately draw the internal bisectors of the angles at Q and R to meet […]
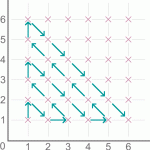
Look at the route the arrows follow in this diagram. Look away from the screen and try to describe their path.
Will the route pass through the point (18,17)?
If so, which point will be visited next? Explain how you found out.
How many points does the route pass through […]
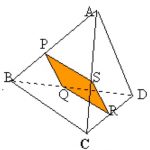
ABCD is a regular tetrahedron and the points P, Q, R and S
are the midpoints of the edges AB, BD, CD and CA.
Prove that PQRS is a square.
What does this tell you about the opposite edges of the tetrahedron?
A triangle has sides 12, 13 and 15 units. Circles are drawn with centres at the vertices of the triangle so that each circle touches the other two.
Find the radii of the circles.
Can you always find touching circles for any triangle?
FOLLOW US ON SOCIAL MEDIA
