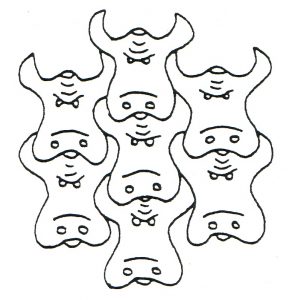
Look at the picture where 7 copies of the bull’s head fit together without any spaces between them. Imagine this pattern extending to infinity. This is called a tessellation or wallpaper pattern. There are only 17 ways that shapes can be repeated to fill the plane.
Draw a repeating pattern with the letter H that is similar to the tessellation of bull’s heads. You could cut out an H-shape made up of 7 squares from card and use it as a template to draw around.
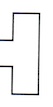
How would you draw the same repeating pattern using the half-H piece? How would you make the same tessellation with quarter-H pieces? What transformations (reflections, rotations and translations) do you see in the way that the single motifs are repeated in the H-tessellation?
The bull’s face is not quite symmetrical so there are no reflections in that repeating pattern, and no rotations. The head is repeated simply by translation.
Fabric or wallpaper the designs may include only geometric shapes, or flowers, animals or anything else. The mathematics of repeating patterns has important applications in 2 and 3 dimensions in crystallography and construction.
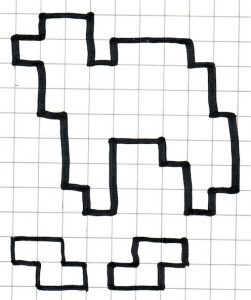Cover the camel with pieces made from 4 squares as shown? Is your solution unique?
Design some tiling patterns with other shapes made up of squares. (You will need paper with a square grid.)
- Find other shapes made from squares that tessellate? Try this using (i) 4 squares as for the camel, (ii) 5 squares (pentominoes) and (iii) 6 squares (hexominoes).
- How many different pentominoes are there? Do they all tessellate? What about hexominoes?
- The H shape above is made from 7 squares. Pick one point in the tessellation of H shapes and mark the point and all its images. What do you notice? Do the same with the bull tessellation.
Click here to download TILING Worksheet 1 for young learners
Click here to download TILING Worksheet 2 for young learners
Click here to download TESSELLATION Worksheet 3
Click here to download TESSELLATION Worksheet 4
Click here to download Worksheet 4 MIRROR MIRROR
If you enjoyed this article, please consider sharing it!
FOLLOW US ON SOCIAL MEDIA
