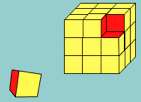
Imagine a large cube made up from 27 small red cubes each measuring 1 cm by 1 cm by 1 cm. What is its volume?
Imagine dipping the large cube into a pot of yellow paint so the whole outer surface is covered. What is its surface area?
Now imagine breaking the […]
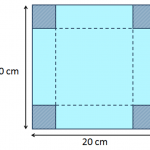
Take a sheet of paper 20 cm by 20 cm and make a box without a lid by cutting out a square at each corner and folding up the flaps. What is the volume of your box?
Make boxes with different volumes by varying the sizes of the squares that you cut […]
The net of a cube has been cut into two. It can be put together in several ways so that it can be folded into a cube.
Here are the nets of 9 solid shapes.
Each net has been cut into 2 pieced like the net of the cube.
Can you see […]
Show that is it impossible to have a tetrahedron whose six edges have lengths 10, 20, 30, 40, 50 and 60 units.
Is it possible for a tetrahedron to have edges of lengths 10, 20, 25, 45, 50 and 60 units?
Can you write general rules for someone else to use to check whether […]
Here you see the front and back views of a dodecahedron which is a solid with pentagonal faces.
Using twenty of the numbers from 1 to 25, each vertex can be numbered so that the numbers around each pentagonal face add up to 65.
The number F is the number of faces […]
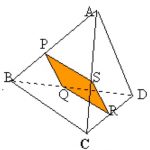
ABCD is a regular tetrahedron and the points P, Q, R and S
are the midpoints of the edges AB, BD, CD and CA.
Prove that PQRS is a square.
What does this tell you about the opposite edges of the tetrahedron?
South Africa COVID-19 News
Here is the official website for COVID-19 updates.
Login
SUPPORT AIMSSEC