Currently viewing the tag: "Polyhedra"
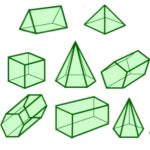
A tetrahedron and an octahedron, both have equilateral triangular faces.
Can you arrange these 8 polyhedra in a line so that every two polys next to each other have a face of the same shape. The matching faces do not need to be the same size.
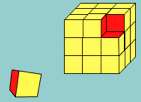
Imagine a large cube made up from 27 small red cubes each measuring 1 cm by 1 cm by 1 cm. What is its volume?
Imagine dipping the large cube into a pot of yellow paint so the whole outer surface is covered. What is its surface area?
Now imagine breaking the […]
Show that is it impossible to have a tetrahedron whose six edges have lengths 10, 20, 30, 40, 50 and 60 units.
Is it possible for a tetrahedron to have edges of lengths 10, 20, 25, 45, 50 and 60 units?
Can you write general rules for someone else to use to check whether […]
Here you see the front and back views of a dodecahedron which is a solid with pentagonal faces.
Using twenty of the numbers from 1 to 25, each vertex can be numbered so that the numbers around each pentagonal face add up to 65.
The number F is the number of faces […]
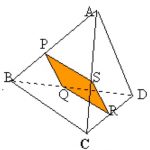
ABCD is a regular tetrahedron and the points P, Q, R and S
are the midpoints of the edges AB, BD, CD and CA.
Prove that PQRS is a square.
What does this tell you about the opposite edges of the tetrahedron?
FOLLOW US ON SOCIAL MEDIA
