Currently viewing the tag: "Multiples"
The lattice points are where the lines intersect. How many interior lattice points do your lines go through?
Draw more grids. Before you draw the diagonals, can you predict how many lattice points they will go through? How do you know?
A point whose […]
What patterns do you notice in this table?
Continue the patterns to fill the empty squares.
Write a list describing all the patterns that you see.
What do you notice about the numbers on squares of the same colour?
Would the patterns […]
How quickly can you find me?
I am a whole number less than 1000.
The product of my digits is 225.
I am not a multiple of 5.
Am I a multiple of 13?
Am I real? Am I rational? Am I irrational?
Now divide me by 11. Is the answer real? […]
These counting games lead to an understanding of multiples and common multiples, number patterns and the Sieve of Eratosthenes to find prime numbers.
Click here to download a pdf with all you need to run your own professional development workshop.
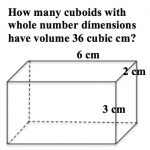
What is the volume of this cuboid?
How many other cuboids with whole number dimensions have the same volume?
Do any of them have the same surface area?
Which has the biggest surface area? Which has the smallest?
How many have a square cross section?
Click here for Notes for Teachers.
[…]
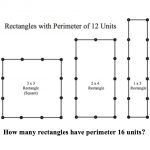
This activity is about rectangles with whole number dimensions. With other lengths and breadths there are infinitely many possible rectangles so here we just stick to whole numbers.
How many rectangles can you make with perimeter 12 units?
What do you know about rectangles? What is the smallest rectangle that you can […]
Describe and explain this pattern.
What do you think the patterns for other multiples look like, for example multiples of 2 or 3 or 4 or 5?
Download this sheet and shade in the patterns of the multiples.
Why do you think that in each pattern […]
Imagine you have four bags containing a large number of 1s, 4s, 7s and 10s.
You can choose numbers from the bags and add them to make different totals. You don’t have to use numbers from every bag, and there will always be as many of each number as you need.
Choose some […]
Is it always possible, from any set of five positive whole numbers, to choose three numbers that add up to a multiple of 3?
For example, if you start with 4, 7, 11, 12 and 18, you can choose 4, 11 and 12 which add up to 27 (a multiple of 3).
[…]
What pattern can you see in the last digits of the powers of 2?
What about the last digits of the powers of 3?
What patterns can you see in the last digits for the numbers in the picture?
Can you explain why all these numbers are multiples of 5?
What about […]
FOLLOW US ON SOCIAL MEDIA
