Polyhedra by Paper Folding

A regular polygon has all its angles equal and all edge lengths equal. In a regular polyhedron all the faces are congruent regular polygons and the same number of polygons meet at each vertex.

Each regular polyhedron has its own codename. The tetrahedron is 333, the octahedron is 3333, the icosahedron is 33333, the cube is 444, and the dodecahedron is 555.

1. Can you crack the code and explain why these codenames have been given to the polyhedra?
2. Use scrap paper and follow the instructions below to make the 5 regular polyhedra by making modules and slotting them together.

CUBE Remove a 17mm wide strip from the short edge of a sheet of A4 so that the ratio of the short to long edges is 210:280 or 3:4. Fold the paper as shown making 2 folds lengthwise and then 3 folds across the strip.   Do the same with three separate sheets of paper, and interlock them to form a cube.

TETRAHEDRON Fold an A4 sheet of paper as shown to make a tetrahedron net (module). Make another identical module, then slot the two together to form a rigid tetrahedron.

[Note: Use scrap paper. The standard size A4 office paper, used very widely worldwide (but not in the USA) has edge lengths in the ratio √2 to 1. Other sizes are in the same proportion, bigger sizes A1, A2 and A3, and smaller sizes A5, A6 etc.  If you do not have A4 paper you can cut your paper in this proportion to make the models.]

OCTAHEDRON Make 4 of the tetrahedron modules as above and flip them over about the vertical edge. Then label the modules as shown. Look carefully at the first and second module. Note that the edge marked ‘A’ and the edge marked ‘B’ each provide a pocket. The corner marked ‘a’ and the corner marked ‘b’ form flaps. Partly fold both modules along the fold lines. Insert flap a into pocket A, and flap b into pocket B. Gently shuffle the two modules together until the two flaps are completely inside the pockets. You have made a square based pyramid, with triangular flaps e and f hanging down on either side.

Take the third and fourth modules. Partly fold bold both modules along the fold lines. Insert flap c into pocket C, and flap d into pocket D. Gently shuffle them together until the two flaps are completely inside the pockets to make another square-based pyramid, with triangular flaps g and h hanging down on either side.

Finally, slide flaps e and f on the first square-based pyramid behind edges E and F on the second pyramid, and at the same time slide flaps g and h on the second square-based pyramid behind edges G and H on the first pyramid. Shuffle the two square bases together until all the gaps close and you have an octahedron.

Click here for more detailed instructions.

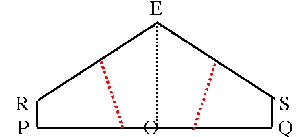
DODECAHEDRON Fold along the red line so that A touches O. Fold C to O similarly. 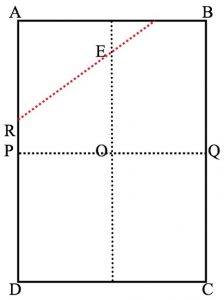Fold B and D to O. Next fold along PQ. Tuck the flap from corner D behind the flat from corner B to make ‘pockets’. Fold R and S up to the centre line EO to make a pentago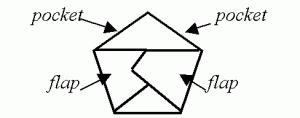n. Make 12 pentagons like this. Assemble them to make a dodecahedron tucking all the flaps into the pockets of adjoining faces.

ICOSAHEDRON From the final stage of the tetrahedron recipe, make the folds shown below to produce a truncated tetrahedron. Make twenty of these truncated tetrahedra and glue them together to form an icosahedron.

Click here for the POLYHEDRA THROUGH PAPER FOLDING Inclusion and Home Learning Guide

Click here for the Notes for Teachers

Click here for the POLYHEDRA BY PAPER FOLDING poster.

Click here for a video giving instructions for making a cube from a square of paper by origami.

Click here for a video giving instructions for making an octahedron from a square of paper by origami.

Parts of this activity are adapted from the NRICH article by Ian Short – Paper Folding Models of the Platonic Solids, with permission of the University of Cambridge. All rights reserved.