PLAY TO LEARN 30-Minute Global Maths and Science Lesson 2024

DOWNLOAD the Maths Week England 2024 30-Minute Lesson details                               

Resources needed: pencil and paper, 5 by 5 grids, 2 sets of cards numbered 1 to 10, envelope or bag.

Warm-up (5 minutes)

For the 3 hand-actions shown, Rock beats Scissors, Scissors beats Paper and Paper beats Rock.

Everyone stands up with, if possible, some space around them.

Everyone plays against the teacher who, on each round, randomly signals scissors, paper or rock. Otherwise the teacher does not take part in the game.

 In the  Side-splits game winners stay still for that round, and losers step to one side with one foot. Players drop out when they lose their balance.

MATHGO is like Bingo but the winner is the first player to get 5 numbers in a line and to explain how the numbers were calculated. Each player makes their own gamecard by drawing a grid and choosing to write on their gamecard 25 numbers between 0 and 100, not repeating any numbers. They cannot change the numbers once they are written on their gamecard.

Each round the caller draws 2 cards at random from a bag, replacing the first before drawing the second, and makes a note of the numbers so the winning card can be checked.

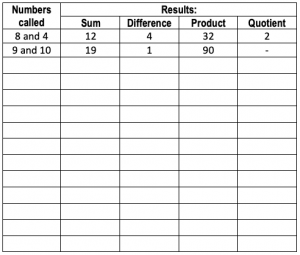Players try to make some of the numbers on their card by combining the two numbers called using one of the operations +, -, × or ÷. If they succeed, they mark the numbers on their gamecard  e.g. 5 and 10 make 15, 5, 50 and 2. The winner is the first player to get 5 numbers in a line and to explain how the numbers were calculated.

Young learners can play with a 4 by 4 grid, aiming to make 4 in a line, combining the numbers on the cards drawn by addition.

Before you play again discuss these questions and encourage players to make a better choice of numbers to put on their cards.

QUESTIONS TO DISCUSS

1. What is the best way to make your own gamecard that gives you the best chance of winning every time you play the game?
2. To make a good choice of numbers for a Mathgo gamecard, can you find how many ways each number from 1 to 100 is formed by combining two numbers using +, -, × or ÷?
3. Which numbers is it impossible to make this way?
4. Are prime numbers a good choice or are some prime numbers a good choice and others a bad choice? Why or why not?
5. On the grid, which squares have 3 or 4 lines through them and which have only two?

Click here for the MATHGO worksheet which includes grids, numbers to cut out and a table for recording.

Click here for the MATHGO Notes for Teachers which includes computer coding to find the frequencies for the numbers to enter on the card. 

FOLLOW-UP

Rock Scissors Paper Game with 5 elements and with 7 elements. This leads to using  2-way tables and showing that the games are fair. https://aiminghigh.aimssec.ac.za/rock-scissors-paper-game/

Mathgo Learners should try to find the best numbers to put on their gamecards and the best arrangement of those numbers. Some learners could write computer code to find the frequencies of results arising as the combinations of two numbers. See the Notes for Teachers in https://aiminghigh.aimssec.ac.za/mathgo/

Holding Mathgo Game played with 3 sets of number cards. Players use combinations of 3 numbers to make numbers to write on their gamecards.

See the AIMING HIGH Let’s Play Mathematically book with 36 collections of games including variations to suit different age groups and to help beginners to learn the rules and the skills involved.

See also the whole collection of AIMING HIGH Mathematical Games